B 树

Last updated Jun 16, 2023

• 数据结构
• 数据库

# B 树

• 数据在硬盘上存储在硬盘块(如4kb block)
• 每一个非叶子节点都有指针 => 很贵
• 在内部可以用二分法快速查找

# B 树的阶 m

1. 每个节点最多有 2m key
2. 每个非根节点最少有 m key, 根节点最少 1 key
3. 一个节点如果有 k key, 就有 k+1 子节点
4. 所有叶子节点在同一层级

max height: $h \leq \lfloor \log_{m+1}(\frac{n+1}{2}) \rfloor + 1$ (n=#key)

# B 树的插入

插入一个 key k

• 找到合适的节点 N

1. 若节点 N 的 key 少于 2m, 则直接插入到 N
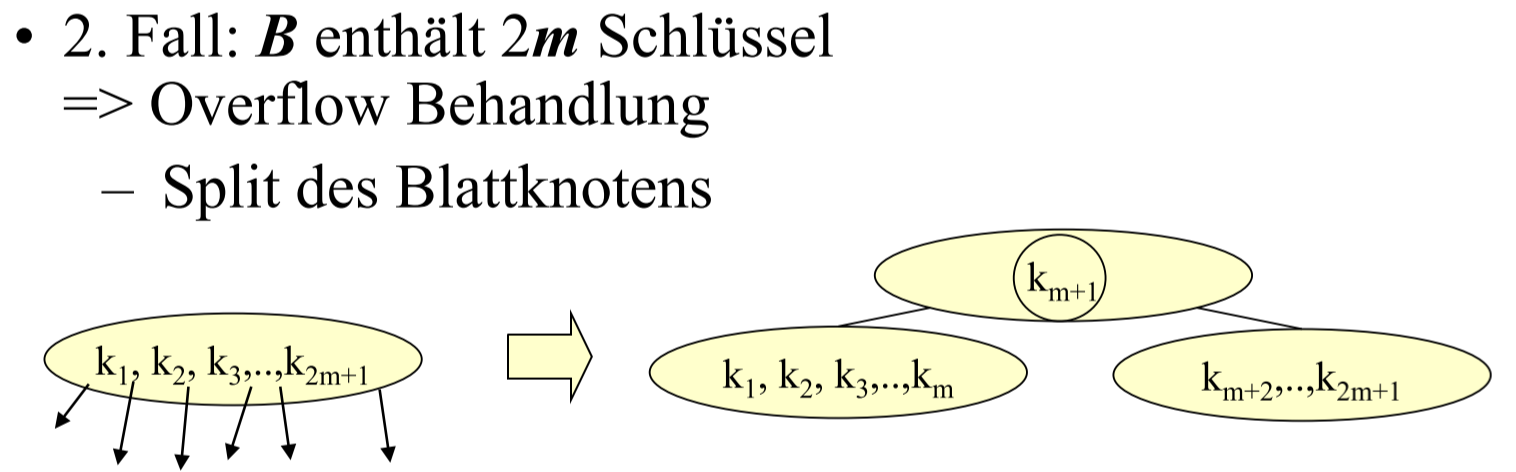
2. 若节点 N 的 key 等于 2m, 则将 N 中的第 m+1 个节点升级为高一级节点(插入到高一级), 原先的 2m 个节点和新来的 k 一起分成两个节点, 作为子节点

# B 树的删除

• 找到对应的节点 N, 并需要观察相邻节点 N+1

1. 若删除后有 #key $\geq$ m , 直接删除
2. 若删除后 #key < m,
   1. 若相邻节点 N+1 的 #key > m, 那就 N 和 N+1 匀一下
   2. 若相邻节点 N+1 的 #key $\leq$ m, 则合并 N 和 N+1