Petri-Netze
Last updated
Jun 17, 2023
属于 lmu - Betriebsystem
# Petri-Netze components
- Petrinetze $$Y = (S,T,F,K,W,M_0)$$
- Stellen S
- Transitionen T
- Kanten F
- Kapizität K einer Stelle
- Kantengewicht W einer Kante
- Marken M
# ·x, x·, -x, x-
- Sei $$ x \in S \bigcup T$$
·x:= $${y \in S \bigcup T : (y, x) \in F }$$
- Vorbereich einer Stelle/Transition x
- 链入x的Stelle/Transitionen
x· := $${ y \in S \bigcup T : (x, y) \in F}$$
- Nachbereich einer Stelle/Transition x
- x链出的Stelle/Transitionen
-x:= $${(y,x) \in (S \times T) \bigcup ( T \times S) : (y,x) \in F}$$
- Menge aller Eingangskanten von x
- 链入x的Kanten
x- := $${(x,y) \in (S \times T) \bigcup ( T \times S) : (x,y) \in F}$$
- Menge aller Ausganskanten von x
- 链出x的Kanten
# Markierung
- Markierung可以理解为状态,下标从0开始
- 形如:
$$M = {0,0,1,0}$$
$$M_1 = {1, 0, 0, 1 }$$
- 注:这个Petri-Netze有4个Stellen, 在M状态时S2有一个Mark, (转换到)M1状态时S0, S3有一个Mark
- Aktivierte Transitionen (在M状态下)可以执行的Transition。
collapsed:: true
- 条件:
- 其Vorbereich有足够的Marken
- 其Nachbereich有足够的空余容量
- Folgemarkierung $M^{’}$: 即经过一次T后(计算得到)的下一个Markierung
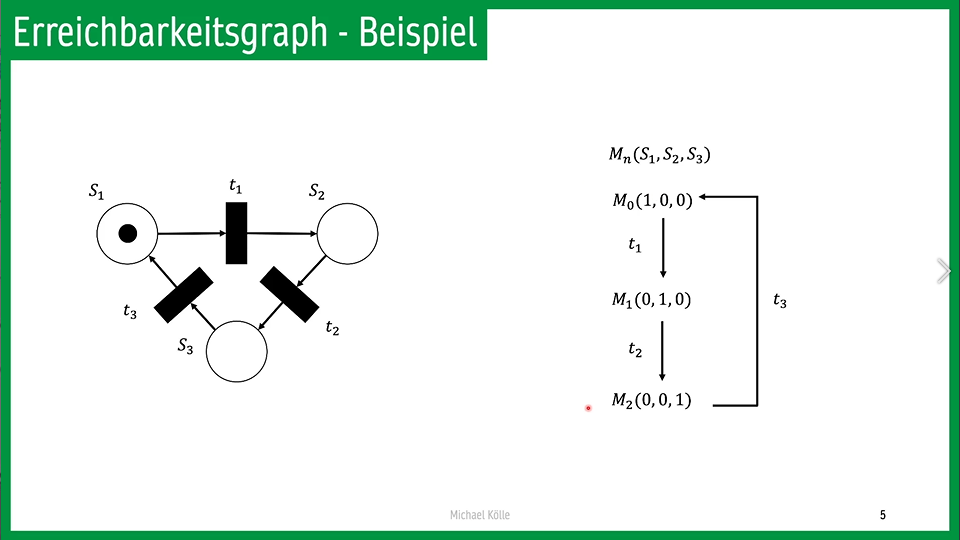
# Erreichbarkeitsgraph
- Die Erreichbarkeitsmenge $E_Y$ zu dem Petri-Netze Y enthält die Anfangsmarkeirung $M_0$:
$$E_Y = E_Y (M_0) := { M^{’}: \exists n \in \mathbb{N_0}, t_1,…,t_n \in T^* : M_0 \xrightarrow{t_1,…,t_n} M^{’} }$$
- 就是从M出发能到的所有Markierung
-
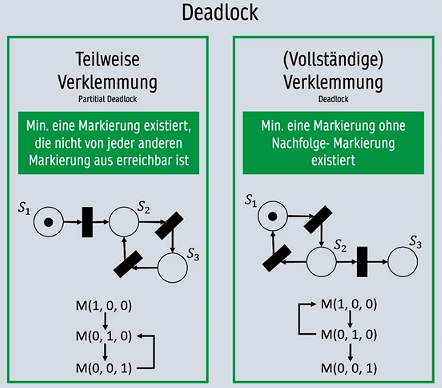
# Deadlock/Verleimmungen
- Teilweise Verklemmung
- Min. eine Markierung existiert, die nicht von jeder anderen Markierung aus erreichbar ist.
- Vollständige Verklemmung
- Min. eine markierung ohne Nachfolge- Markierung existiert.
-
# How to draw a Petrinetze
- 每个 Object 的每个状态需要一个 Stelle
- 每多一个 Ressouce,就需要一个 Stelle。权限也算做Ressouce

