3Blue1Brown - 线性代数的本质
作者:3Blue1Brown 来源:Bilibili
# 01 - 向量究竟是什么?What exactly a vector is
- (在坐标轴里,物理学角度),向量是沿着某个特定方向的运动。这就可以解释两个向量相加为什么是头尾相连。
- 向量数乘被称作 scaling 缩放,而用于缩放的数字称为 scalars 标量。
- 线性代数围绕两种基本运算:向量加法和向量数乘
# 02 - 线性组合、张成的空间与基 Linear combinations, span, and bases
- 另一个视角:把向量看成标量 $\hat{\imath}, \hat{\jmath}$ 的延伸(伸展)
- $\hat{\imath}$ 是[1,0], $\hat{\jmath}$ 是 [0,1],两者是基向量, basis vectors
- 如果选择两个新的基向量(两个基向量要不在一条线是上)(也不能的是零向量)
- 给定向量的张成空间span, 即给定向量通过线性组合( $a\vec{v} + b\vec{w}$ )能形成的向量的集合
- 换句话说,通过对给定向量的向量加法和向量数乘能得到的向量集合
- 三维空间中两个不共线的向量的张成空间是一个平面,而三个不共面的向量的张成空间整个三维空间
- **线性相关(linear dependent)**的向量指的就是二维共线或者三维共面的向量,他们不能张成更多的空间,是多余的
- **线性无关(linear independent)**的向量能够张成空间添加新的维度
- 向量空间的一组基(basis)是张成该空间的一个线性无关向量集
# 03 矩阵如同线性变换 Matrices as Linear transformations
# Linear transformation
- transformation -> function
- input-output relation
- “transformation” for movement: move input vector to output vector
- linear: line remains line, without curves; origin remains fixed. -> Grid lines remain parallel and evenly spaced(保持平行并等距分布)
- 线性变换实际上是改变基向量
-
线性的(准确)定义


-
一个 2x2 矩阵实例
- 已知 $\vec{v} = \left[ \begin{array}{c} -1 \\ 2 \end{array} \right]$ , 即 $\vec{v} = -1\hat{\imath} + 2\hat{\jmath}$
- 应用线性变换 $\hat{\imath} = \left[ \begin{array}{c} 1 \\ -2 \end{array} \right], \hat{\jmath} = \left[ \begin{array}{c} 0 \\ 3 \end{array} \right]$
- 则此时 $\vec{v} = -1\hat{\imath} + 2\hat{\jmath} = -1\left[ \begin{array}{c} 1 \\ -2 \end{array} \right] + 2\left[ \begin{array}{c} 0 \\ 3 \end{array} \right] = \left[ \begin{array}{c} 5 \\ 2 \end{array} \right]$
- 写成矩阵计算就是 $\left[ \begin{array}{cc} 1 & 3 \\ -2 & 0 \end{array} \right] \\ \left[ \begin{array}{c} -1 \\ 2 \end{array} \right] = \left[ \begin{array}{c} 5 \\ 2 \end{array} \right]$

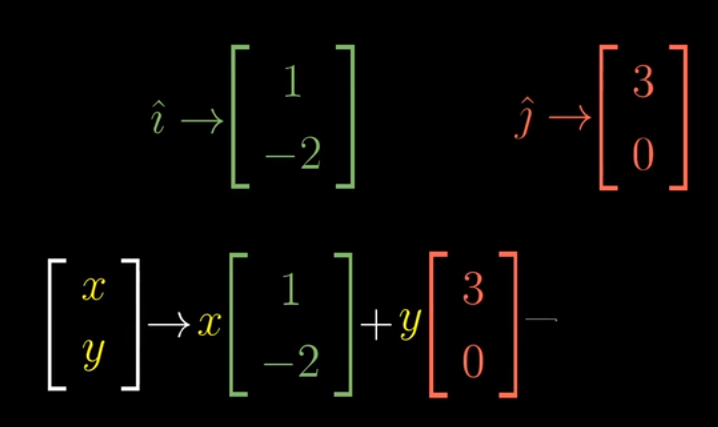
-
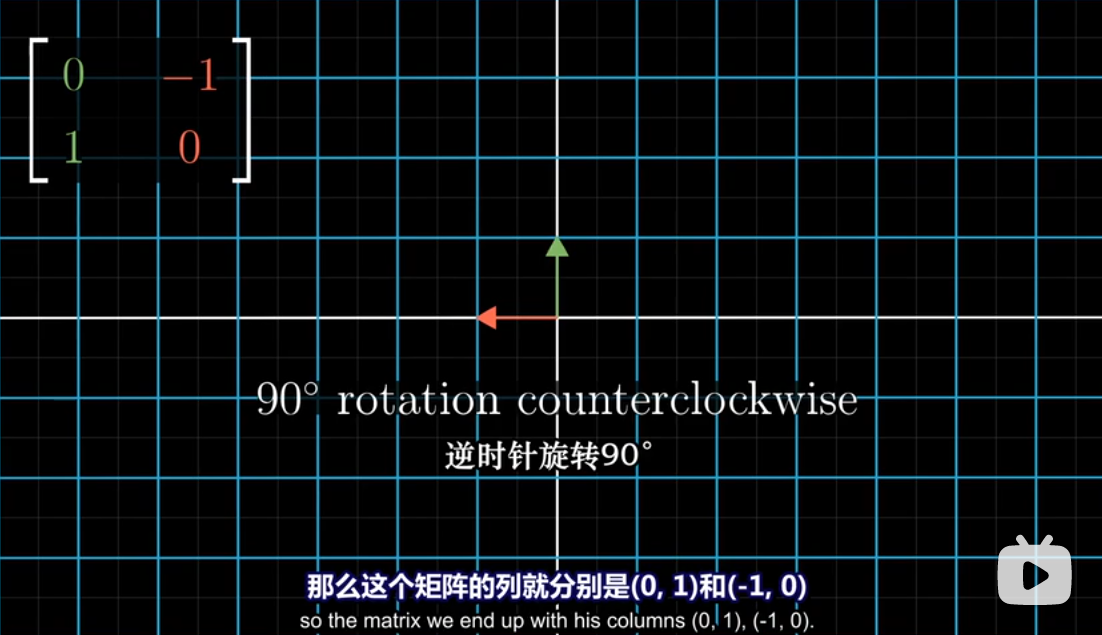
所以你可以很容易地看出旋转
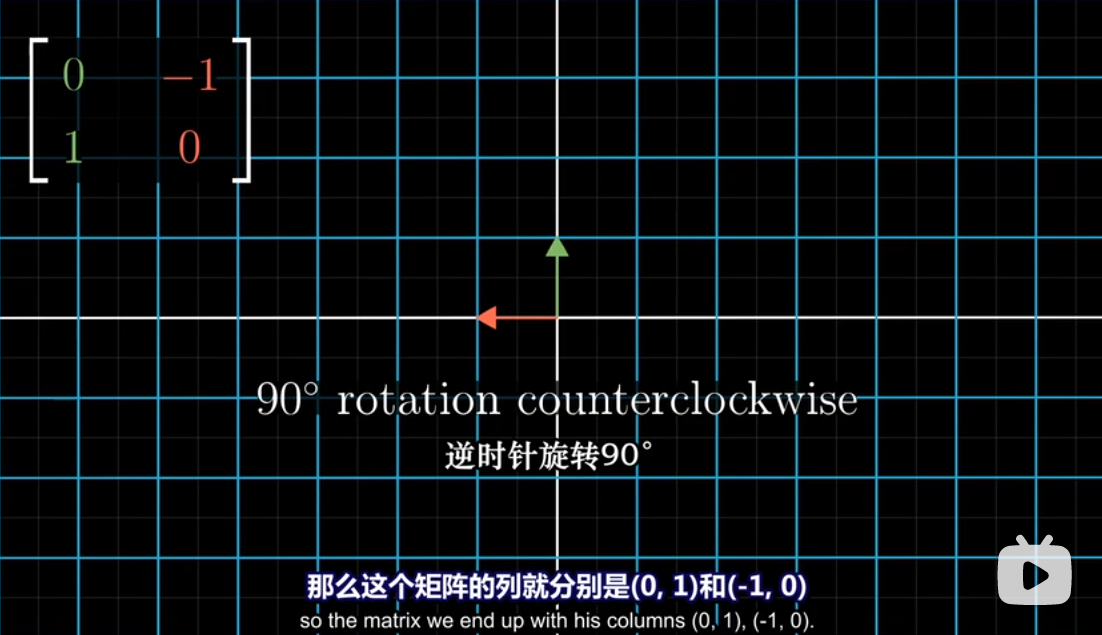

-
行和列的线性相关也很容易想象
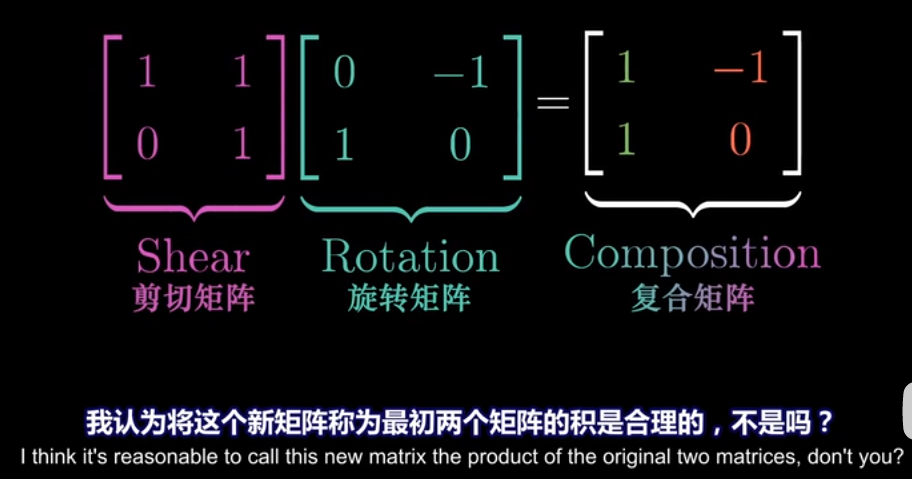
# 04 矩阵乘法与线性变换复合 Matrix multiplication as composition
- 两个矩阵相乘可以看作两次连续的线性变换
-
如果两个线性变换组合的效果和一个线性变换的效果相同
-
那么这两个线性变换的矩阵相乘等与另一个线性变换的矩阵
-
变换的顺序是从右往左

-
- 矩阵乘法满足结合律:线性变换的顺序不会影响结果
# 附注1 三维空间中的线性变换 Linear transformations in three dimensions
# 05 行列式 The determinant
- 线性变化后,某一特定区域的面积如何变化?
- 行列式的值就是面积变化的倍数
- 或者说,一个 m行n列的行列式,计算的是 n个m维向量围成的空间大小
- 想知道行列式的值是否为0,只要看是否线性相关(二维的时候面积为0,三维的时候体积为0)
- 如果行列式的值出现负数,说明整个空间被翻转过了(The Orientation has been reversed)
- Parallelepiped 平行六面体
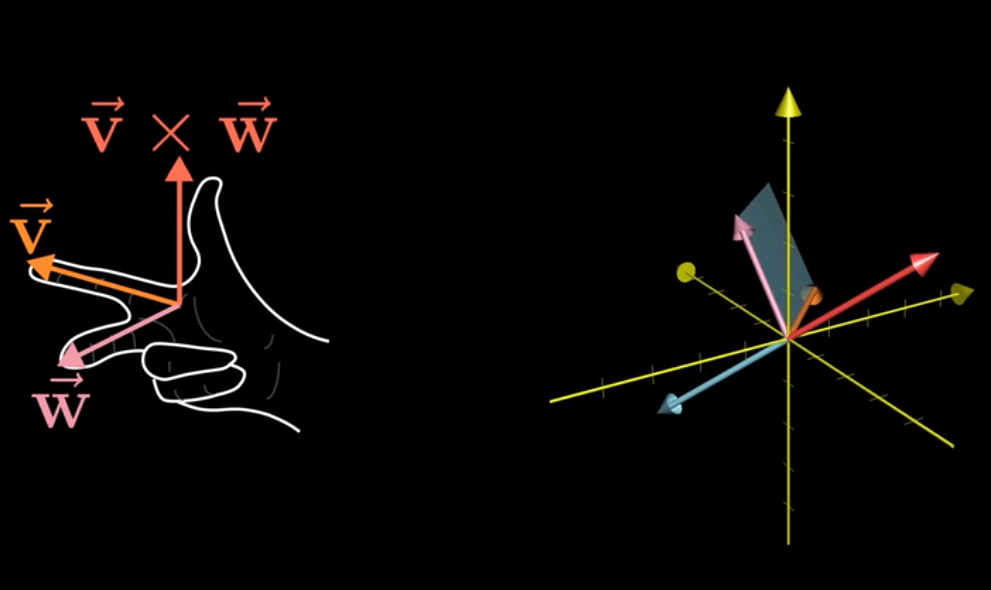
- 三维中的正方向需要用到右手定则:食指 $\hat{\imath}$ , 中指 $\hat{\jmath}$ , 拇指 $\hat{k}$
- 行列式计算公式理解
-
如果 b, c 都为 0,放大的倍数就像计算正方形
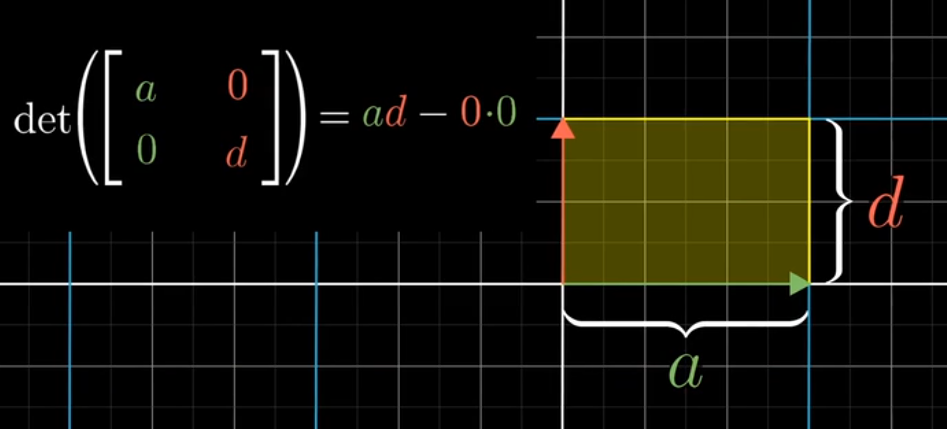
-
如果只有 b 为 0,平行四边形的计算公式还是一样的
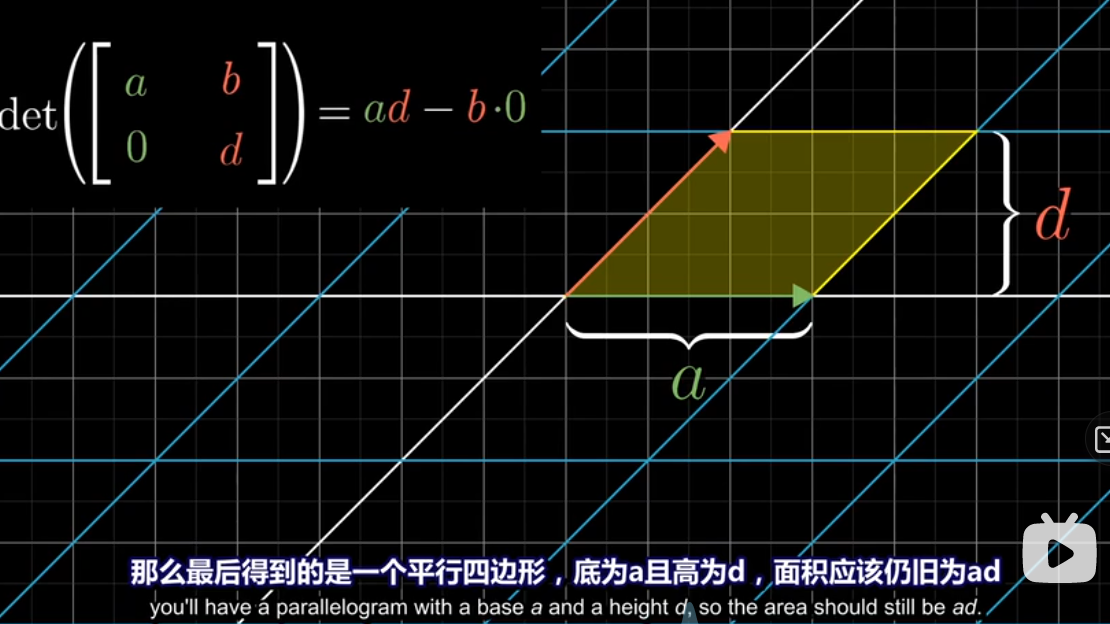
-
如果你想思考全不为0
- 下面的行列式即是在计算黄色部分的面积
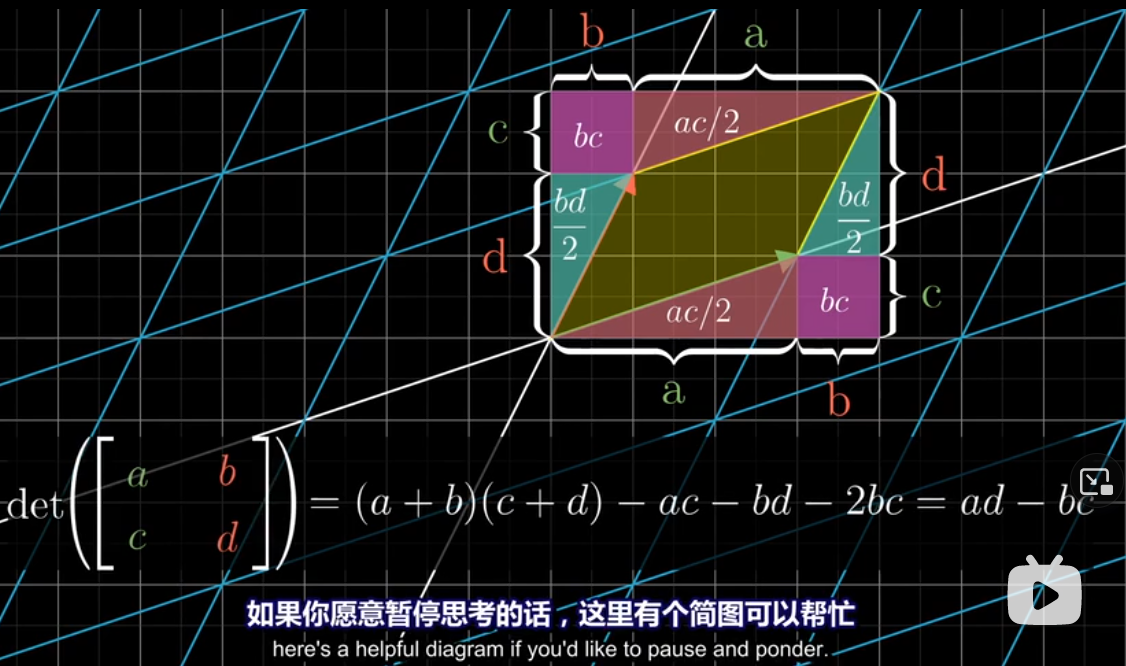
- 下面的行列式即是在计算黄色部分的面积
-
平行六面体的体积
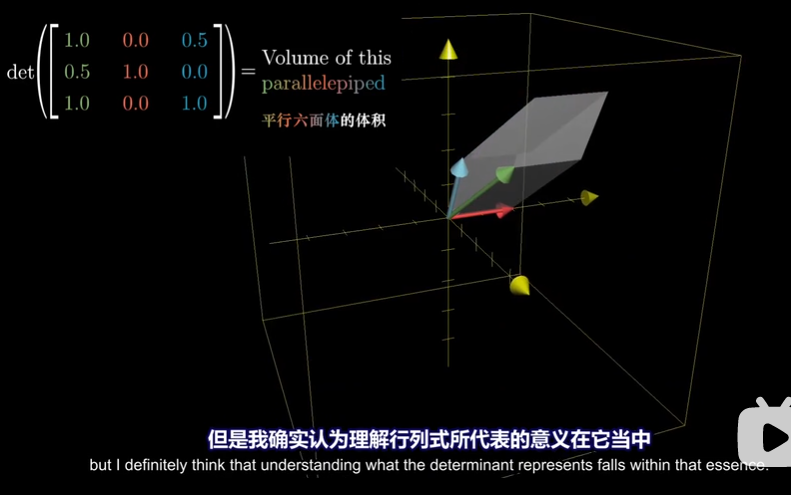
-
行列式的计算

-
# 06 逆矩阵,列空间,秩与零空间 Inverse matrices, column space, rank and null space
- 高斯消元法 Gaussian elimination
- 行阶梯型 Row echelon form
- 线性方程组 Linear system of equations
- $A\vec{x} = \vec{v}$ 的含义:寻找一个未知向量 $\vec{x}$ , 使得 向量 $\vec{x}$ 在经过矩阵 $A$ 的线性变换后,与向量 $\vec{v}$ 重合
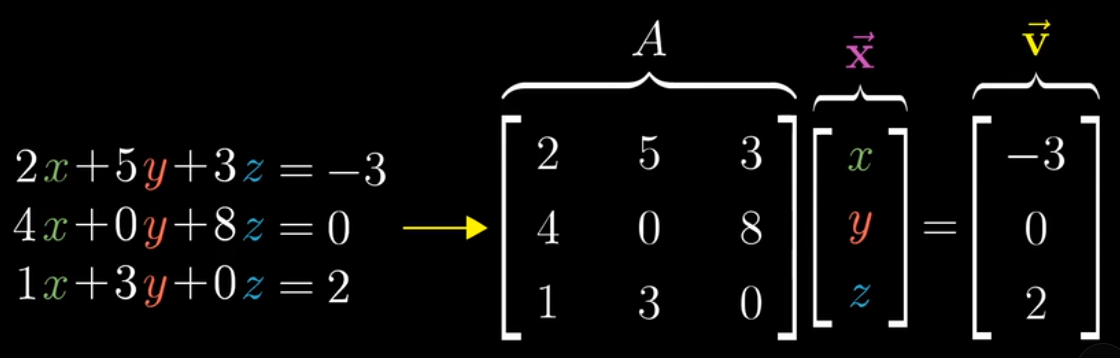
- 因此,如果矩阵的秩小于列数,或者行列式等于0(相当于线性变换会导致降维),这个线性方程组是无解的
- 所以: $\det(A) \neq 0$ -> $A^{-1}\\ exists$ , 没有逆矩阵的矩阵就是降维了
- 但 $\det(A) = 0$ 时依然可能有解,这是因为向量 $\vec{v}$ 刚好就落在降维后的空间里

- 但 $\det(A) = 0$ 时依然可能有解,这是因为向量 $\vec{v}$ 刚好就落在降维后的空间里
- $A\vec{x} = \vec{v}$ 的含义:寻找一个未知向量 $\vec{x}$ , 使得 向量 $\vec{x}$ 在经过矩阵 $A$ 的线性变换后,与向量 $\vec{v}$ 重合
- 逆矩阵就是逆向的线性变换
- 比如说顺时针旋转90度的逆矩阵就是逆时针旋转90度
- 秩
- 秩:输出空间的维数。一个n维矩阵最大的秩是n,这时称这个矩阵满秩(full rank)
- rank 1 = line, rank 2 = plane, rank 3 = space
- 列空间
- 列空间 Column space <=> 列张成的空间 span of columns
- 秩更精确的定义是列空间的维数
- 零向量一定在列空间中,因为原点fixed
- 零空间
- = Null space = 核 Kernel
- 变换后落在原点的向量集合,被称为矩阵的零空间或核
- $A\vec{x} = \vec{v}$ 中,如果 $\vec{v}$ 是零向量,那零空间就是 $\vec{x}$ 的所有解
# 附注2 非方阵 Nonsquare matrices
- 非方阵,比如3x2矩阵,就是把二维的两个基向量,转转两个三维基向量
# 07 点积与对偶性 Dot products and duality
-
几何解释
- 将 $\vec{w}$ 投影在 $\vec{v}$ 所在的直线,将 $\vec{w}$ 的投影长度与 $\vec{v}$ 的长度相乘
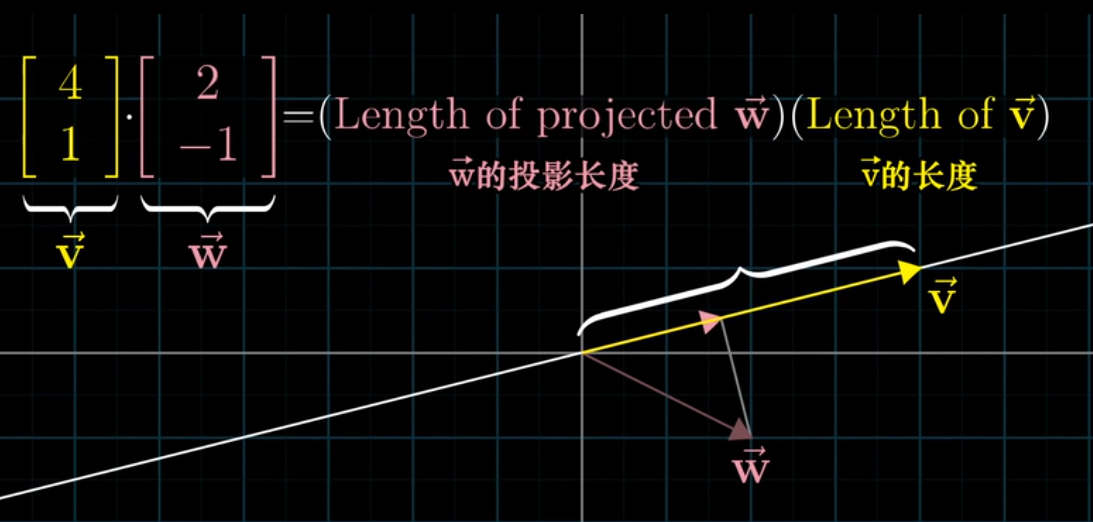
- 所以当两个向量垂直时,点积是0
- 将 $\vec{w}$ 投影在 $\vec{v}$ 所在的直线,将 $\vec{w}$ 的投影长度与 $\vec{v}$ 的长度相乘
-
Scaling 对点积的影响是线性的
-
矩阵向量乘积与点积的关系
- 将二维向量投射到数轴上,数轴的基向量是 $\hat{u}$

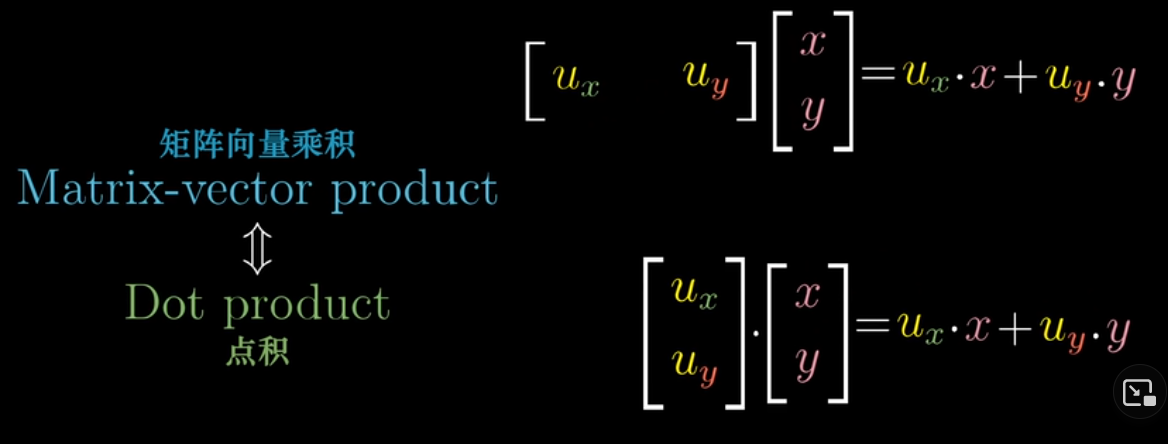
- 将二维向量投射到数轴上,数轴的基向量是 $\hat{u}$
-
对偶性 Duality
- super tricky to define
- 自然而出乎意料的对应关系
- 每当你看到一个(多维)空间到数轴的线性变换时,它都与那个空间的唯一的向量相关
# 08 以线性变换的眼光看叉积 Cross products in the light of linear transformations
-
正方向
- 乘号右边的向量在左边的向量的逆时针方位时得到的面积为正
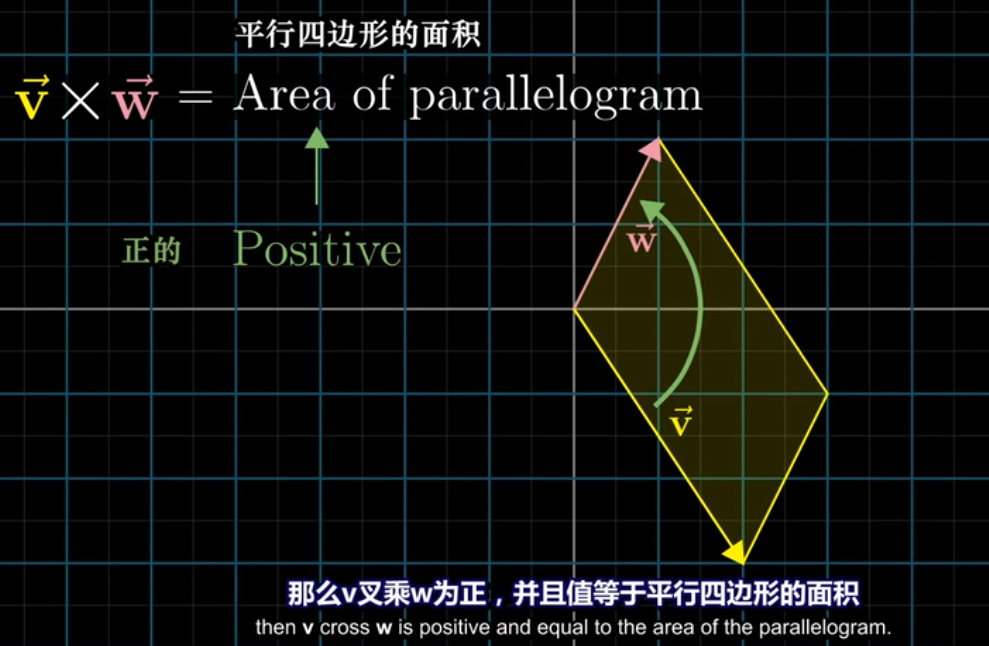
- 这个式子计算出的面积也等同于将两个向量列成2x2矩阵,计算行列式得到的值
- 乘号右边的向量在左边的向量的逆时针方位时得到的面积为正
-
真正的叉积是通过两个三维向量生成一个新的三维向量
-
用行列式计算叉积


-
理解这个变换

- 将第一个向量看成变量,得到一个线性函数
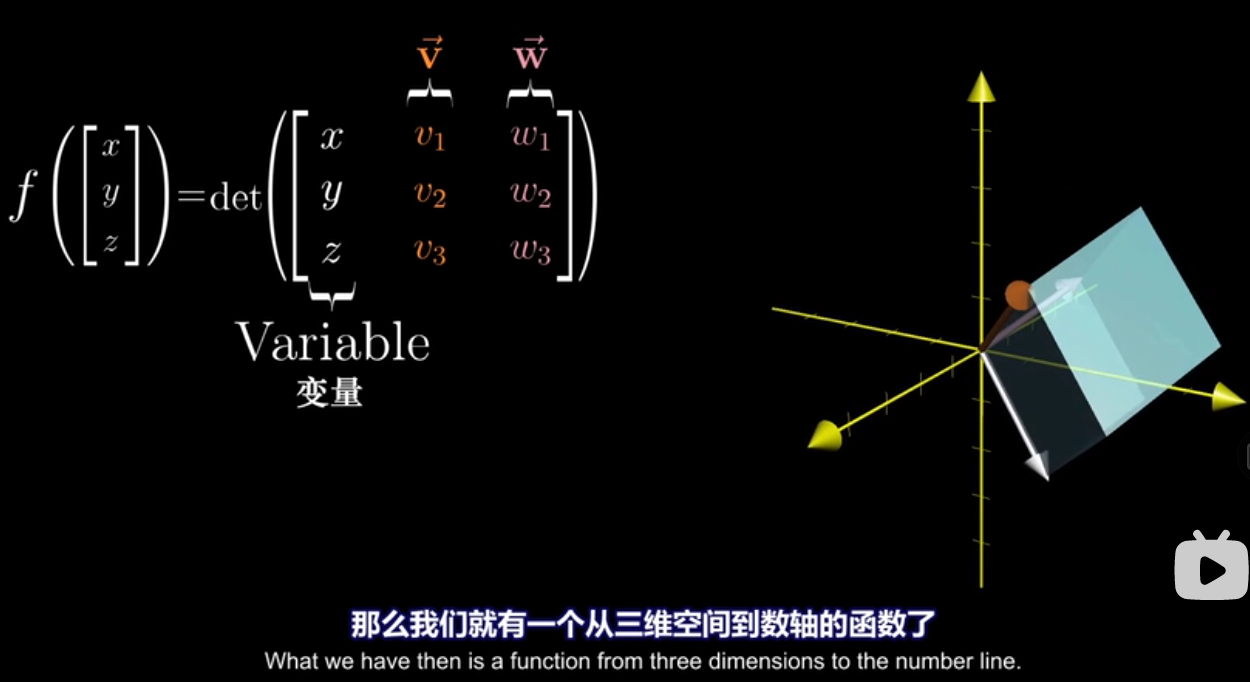
- 找到一个 $\vec{p}$ , 使得

- 将第一个向量看成变量,得到一个线性函数
-
我们找到的这个 $\vec{p}$ , 在看起来是这样的,垂直于 $\vec{v}$ 和 $\vec{w}$ 形成的平面。将向量变量(白)投影到 $\vec{p}$ 所在的直线上,就能计算这个平行六面体的体积
# 09 基变换 Change of basis
-
如何转化两个基向量不同的坐标系统
- 我们用了标准基向量,Jennifer: $\hat{\imath} =\left[ \begin{array}{c} 2 \\ 1 \end{array} \right], \hat{\jmath} = \left[ \begin{array}{c} -1 \\ 1 \end{array} \right]$
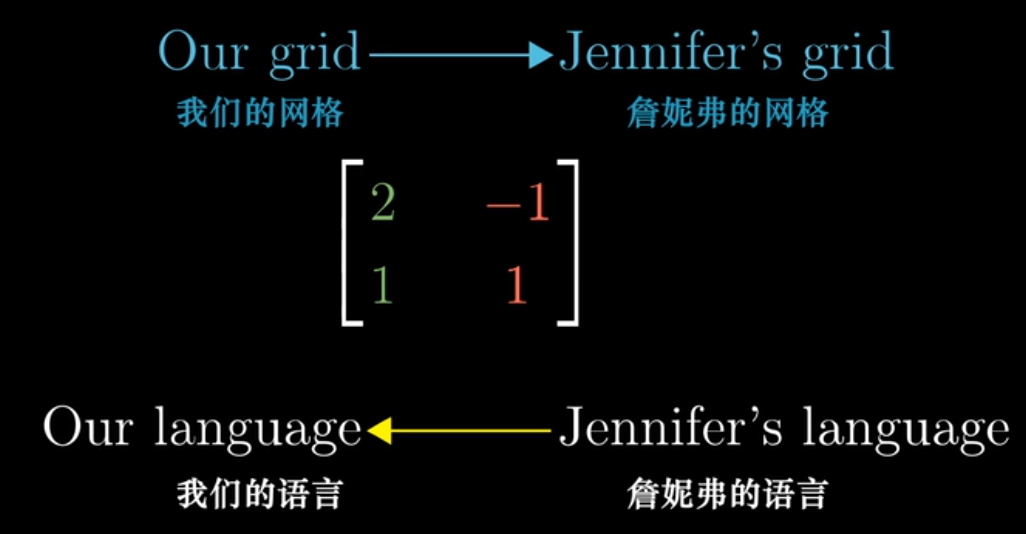
- 向要反过来就求这个矩阵的逆矩阵
- 我们用了标准基向量,Jennifer: $\hat{\imath} =\left[ \begin{array}{c} 2 \\ 1 \end{array} \right], \hat{\jmath} = \left[ \begin{array}{c} -1 \\ 1 \end{array} \right]$
-
旋转90度如何转化给另一个坐标系统
- 在自己的坐标上逆时针旋转90度,也就是乘上 $\left[ \begin{array}{cc} 0&-1 \\ 1&0 \end{array} \right]$
- 需要
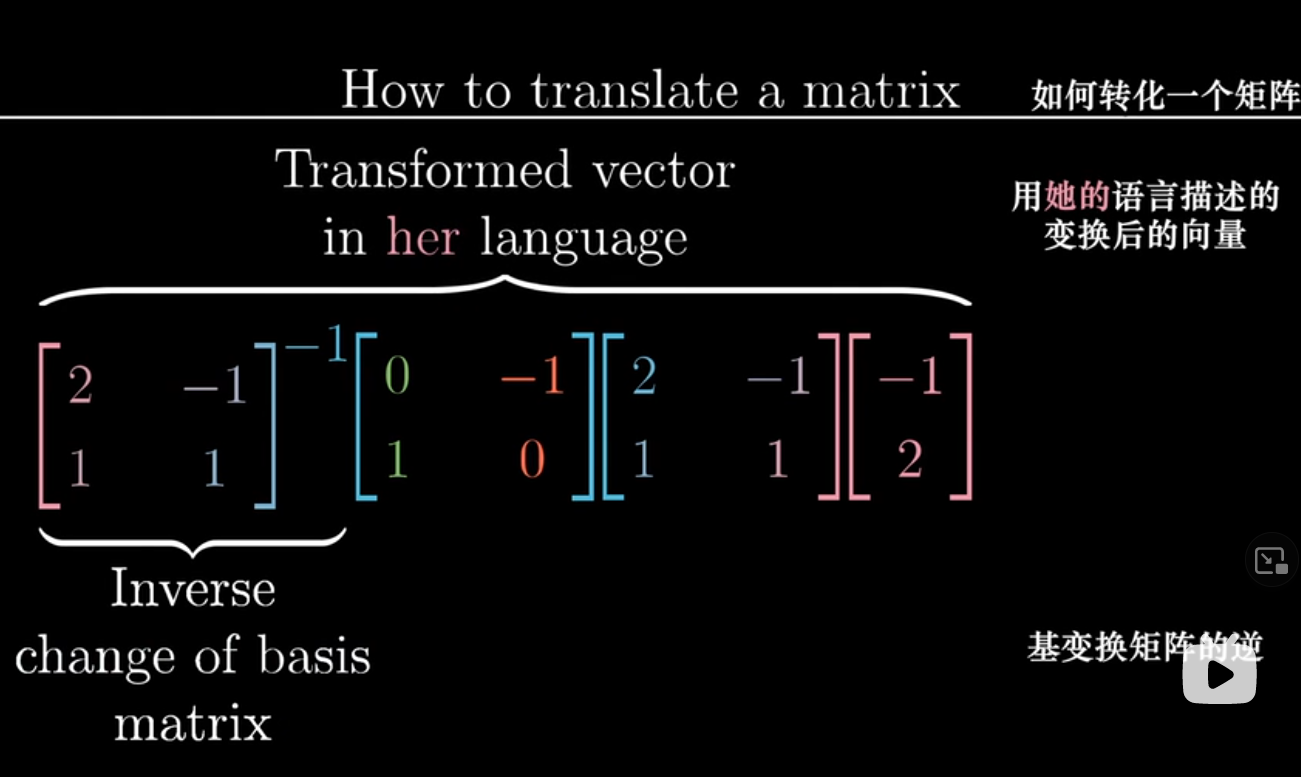
- 用我们的语言描述对方的坐标系统
- 应用变换矩阵
- 用对方的语言描述这个结果
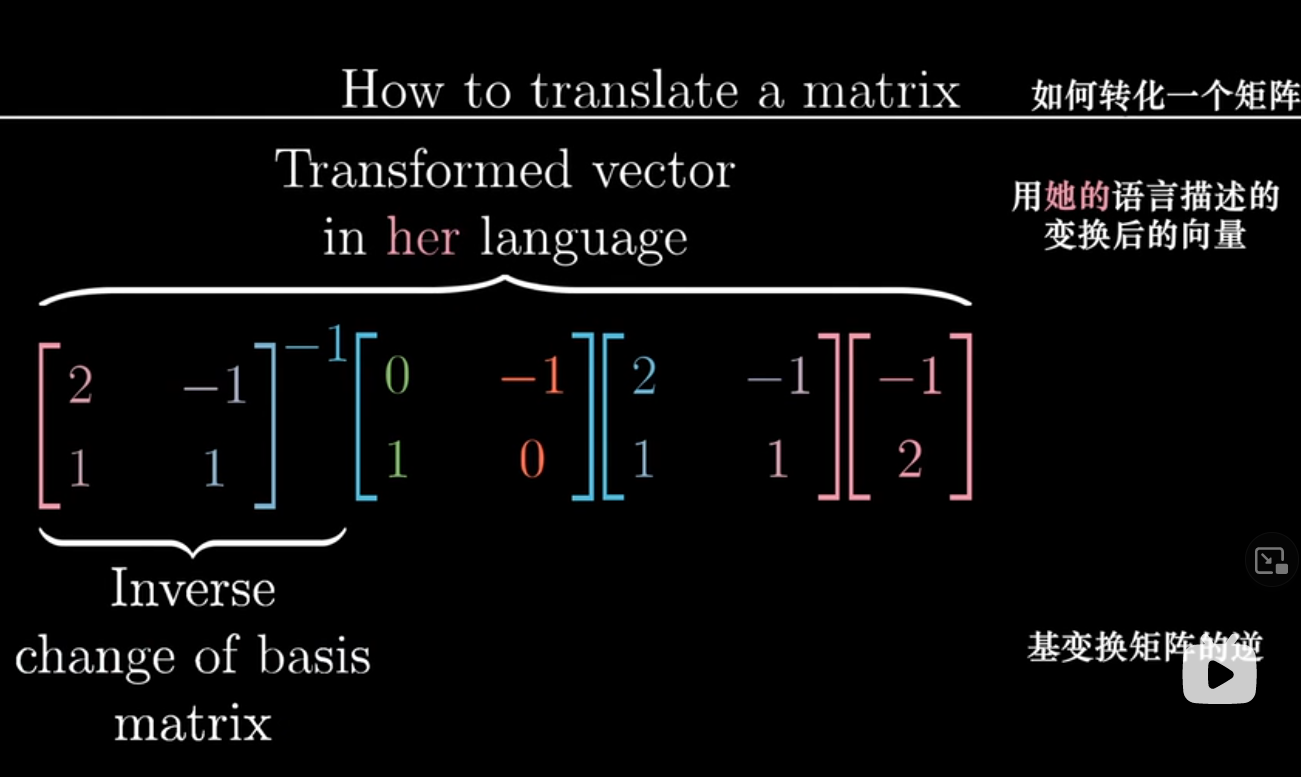
- 前三个矩阵相乘,可以看做直接应用的函数/变换矩阵
-
表达式 $A^{-1}MA$ 按时了一种数学上的转移作用
# 10 特征向量与特征值 Eigenvectors and eigenvalues
-
要求基础知识牢固
-
向量在空间变换后通常会离开它原本张成的空间
-
特殊的向量不会离开,如 $\hat{\imath}$
-
矩阵的特征向量,就是这些特殊向量,在变换之后不离开原本张成的直线。特征向量不一定存在
-
特征值,就是特征向量在变换中拉伸或压缩比例的因子,可以为负
-
三维空间中,特征向量就是变换的旋转轴
- 旋转的特征值必定为1
- 说绕着某某向量旋转多少度,比给出一个旋转的变换矩阵,直观得多
-
求矩阵 $A$ 的特征向量和特征值
- 即求解 $\lambda$ 和 $\vec{v}$ ,使下面这个等式成立

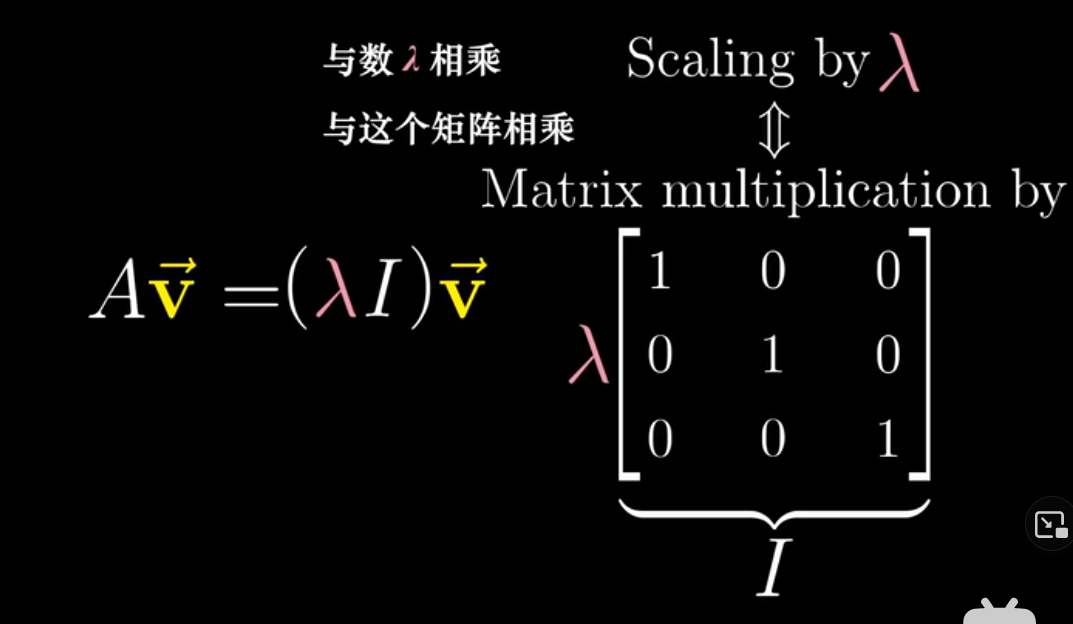

- $\vec{v}$ 非零,所以需要找一个特征值 $\lambda$ , 使行列式为0,也就是将空间降维

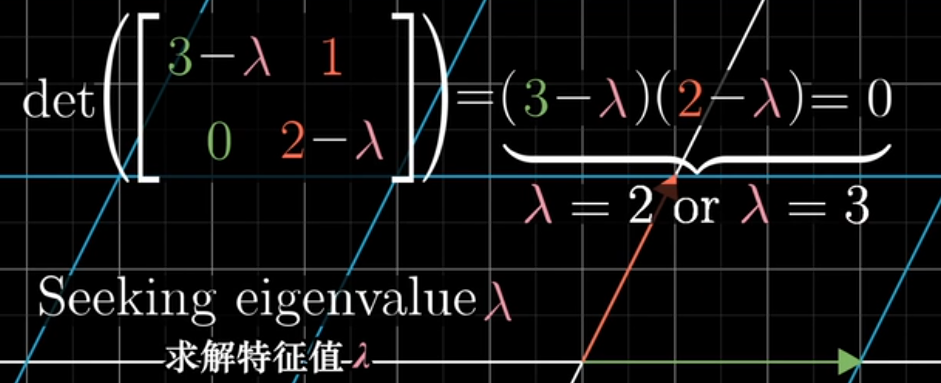
- 即求解 $\lambda$ 和 $\vec{v}$ ,使下面这个等式成立
-
特征基,基向量也是特征向量,这时候计算很容易。因为都是缩放操作,变换矩阵是对角矩阵
# 11 抽象向量空间 Abstract vector spaces
函数也可以看作向量乘法 - 比如一个 xxx 的多项式,选定关于 xxx 的基函数为 b0(x)=1b_0(x) = 1b0(x)=1, b1(x)=xb_1(x) = xb1(x)=x, b2(x)=x2b_2(x) = x^2b2(x)=x2, … - 然后以系数为变量,基函数为基向量
函数的空间性: 比如上一个例子中,当前空间就是全体多项式
求导(derivative) 是线性运算
把求导运算转换成矩阵(线性变换)是这样的

-
向量是什么:如果要让已经建立和的理论和概念适用于一个向量空间,那么它必须满足八条公理

问向量是什么就好像问数字3是什么一样