Project Asteria
Last updated
Jun 17, 2023
# 微积分
- 求一个函数的倒数,就是求它的斜率,因此有 $\frac{dy}{dx} = \frac{f(x+\Delta x)-f(x)}{\Delta x}$
- 求导 differentiate 是一个 线性算符 linear operator
- 幂函数 $f(x)=x^{n}$, 导数是 $nx^{n-1}$
- Product rule 的推导跟面积是类似的:
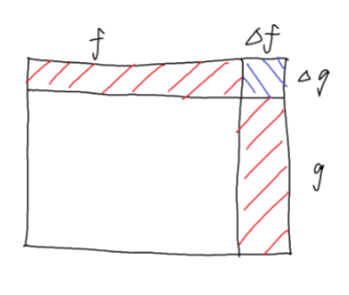
- $\Delta S = f \cdot g + f \cdot \Delta g + \Delta f \cdot g$
- 有了Product rule,就能用 $\frac{d}{dx} (f(x) \cdot \frac{1}{g(x)})$ 推出Quotient rule
- $e^{x}$: 自然对数$e^{x}$的导数为什么是它本身?将 $\exp x$ 展开求导就知道了$$\exp(x) = \sum^{\infty}_{n=0}\frac{x^n}{n!}$$
- $ln(x)$ : 已知 $e^{x}$ 的导数的导数是它本身,就能求其反函数 $ln(x)$ 的导数:
- 令 $y=exp\\ x$ , 则 $x=ln\\ y$
- ∵ $\frac{dy}{dx} = exp\\ x$
- ∴ $\frac{dx}{dy} = \frac{1}{exp\\ x} = \frac{1}{y}$
- $\partial$ 称为偏微分算符, 强调对多元函数的求导(其实和微分算符没什么区别)
- 同上反函数的求导法,可以用三角函数的导数得到反三角函数的
- 1.8讲了个对方程求导的黑科技:把方程的两边对同一个自变量求导,方程仍然成立
- $y=x^{x}$ (求对数)
- $ln\\ y = x\\ ln\\ x$ (两边对x求导)
- $\frac{1}{y} \cdot \frac{dy}{dx} = ln\\ x + 1$
- $\frac{dy}{dx} = y(ln\\ x+1) = x^{x}(ln\\ +1)$
- 也可以用来解椭圆的切线
- 椭圆公式 $\frac{x^{2}}{a^2} + \frac{y^2}{b^2} = 1$
- 什么函数可以求导?断掉的(不连续), 爆掉的(趋于无限, blow up)
- 对没有断的分段函数,计算分割点的两边的导数,如果相同,就在分割点上可求导
# 复变函数与级数
- $\sin\\ x$ 和 $\cos\\ x$ 用$\exp\\ x$表示出来
- $\sin\\ x = \frac{1}{2i} (e^{ix} - e^{-ix})$
- $\cos\\ x = \frac{1}{2} (e^{ix} + e^{-ix})$
- 把虚数去掉,就变成了双曲正弦函数和双曲余弦函数
- $\sinh\\ x = \frac{1}{2} (e^{x} - e^{-x})$
- $\cosh\\ x = \frac{1}{2} (e^{x} + e^{-x})$
- 关系
- $\sin\\ x = -i\\ \sinh\\ ix$
- $\sinh\\ x = -i\\ \sin\\ ix$
- $\cosh\\ x = \cos\\ ix$
- $\cos\\ x = \cosh\\ ix$
- $\frac{d}{dx} \sinh\\ x = \cosh\\ x$
- $\frac{d}{dx} \cosh\\ x = \sinh\\ x$
- $\sin (x+y)$ 展开式的作图推导
https://zhidao.baidu.com/question/33089867
- 把三角函数表示成指数可以方便地推导积化和差公式
- 如 $\sin\\ a\\ \sin\\ b = \frac{1}{2} (- \cos(a + b) + \cos(a - b))$
- 级数是将数列的项依次用加号连接起来的函数
- 泰勒级数。它求导就会发现它满足“x = 0 处的值和任意阶导数都与ln(1 + x) 相等”这个条件。泰勒级数的思想可以看妈咪说的泰勒展开式讲解
- 小量近似的一个思想是,在 $|x|\ll 1$ 时,可以把高阶项忽视,只剩下 $a_0 + a_1 x$
- 当然,每多保留一项就会更精确一点
- 小量计算的重要公式 $(1+x)^n = 1+ nx$
- 【练习】求exp ln(1 + x) 的泰勒级数,保留到三阶。结果当然是1 + x。
# 微分方程
- 补课 常系数线性微分方程
- 补课 费曼物理学讲义第一卷
# 线性代数
- 建议阅读: 3Blue1Brown - 线性代数的本质
- 矩阵乘法不满足交换律, 但满足结合律
- 坐标的旋转操作:
- 如果用矢量 $\mathbf{P} = \left[ \begin{array}{c} x_p \\ y_p \end{array} \right]$ 表示 $P$ 的坐标,
- 矩阵 $\mathbf{R}(\theta) = \left[ \begin{array}{cc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right]$ 表示旋转操作(它的元素是 $\theta$ 函数),
- 那么 $P$ 旋转后的坐标 $\mathbf{P^{\prime}} = \mathbf{R}(\theta)\mathbf{P}$
- 这是为什么呢?原理就和 $\sin(x+y)$ 以及 $\cos(x+y)$ 是一样的. 或者证一下 $\mathbf{R}(a)\mathbf{R}(b) = \mathbf{R}(a+b)$ 就明白了
- 坐标的缩放操作:
- $\mathbf{S} = \left[ \begin{array}{cc} 2&0 \\ 0&1 \end{array} \right]$, $\mathbf{SP}$ 表示 x 坐标放大两倍, y 坐标不变
- $\mathbf{S^{\prime}} = \left[ \begin{array}{cc} 1&0 \\ 0&2 \end{array} \right]$, $\mathbf{S^{\prime}P}$ 表示 y 坐标放大两倍, x 坐标不变
- 这样表示后就可以进行连贯操作:
- $\mathbf{P^{\prime}} = \mathbf{R}(\phi)\mathbf{S}\mathbf{R}(\theta)\mathbf{P}$
- 表示: 把 $P$ 旋转 $\theta$ 度, 把 x 坐标放大两倍, 再旋转 $\phi$ 度得到 $\mathbf{{P^{\prime}}}$. 虽然直观上应该从右往左计算, 但矩阵满足结合律, 于是可以从左往右
- 矩阵的换行换列操作:
- $\mathbf{A} = \left[ \begin{array}{cccc} 0&0&x&0 \\ y&0&0&0 \\ 0&z&0&0 \\ 0&0&0&1 \end{array} \right]$
- $\mathbf{AB}$ 表示, 将 B 矩阵第 3 行 乘 x 换到第一行, 第 1 行乘 y 换到第二行, 第 2 行乘 z 换到第三行, 第4行不变
- $\mathbf{BA}$ 表示, 将 B 矩阵第 3 列 乘 x 换到第一列, 第 1 列乘 y 换到第二列, 第 2 行乘 z 换到第三列, 第4行不变
- 变换矩阵 A 第 i 行 j 列的 1 表示(AB为例) 将 B 矩阵的 第 i 行换成 原本第 j 行
- 可以加入连贯操作套餐
- 有一天爱因斯坦说:两个矩阵相乘,如果有相同的下标就表示求和,求和号可以不写. 比如 $C_{ik} = \sum_{j} A_{ij}B_{jk}$ 可以写成 $C_{ik} = A_{ij}B_{jk}$
- 对一个矩阵求导, 相当于对矩阵中的每个元素分别求导
- 对两个矩阵的乘积求导,, 跟对两个数的乘积求导是一样的
- 如果两个矩阵 $\mathbf{A}$ 和 $\mathbf{A^{\prime}}$ 相乘得到 单位矩阵 $\mathbf{I}$ , 那么 $\mathbf{A}$ 和 $\mathbf{A^{\prime}}$ 互为逆矩阵
- 三阶行列式 $$ \left| \begin{array}{ccc} a&b&c \\ d&e&f \\ g&h&i \end{array}\right| = aei + bfg + cdh - ceg - afh - bdi$$ (+\-/)
- 截止 4.5的第一页
[source]
