lmu - Database system
dbs
# Organization
- jede Woche Übungsblatt
- Tut ab 3. Woche
# Einführung
Arbeitsspeicher?
- 主内存, 电脑上内存条那个
- persistent speichern müssen
- Arbeitsspeicher nicht gross genug
Virtueller Speicher?
- 从硬盘里扣出来暂时用一下的
- nicht ausreichen: von der Persistenz zu denken
# 数据库的内容
- Database Schema
- 描述可能的数据
- 元数据, 数据的结构和类型
- 可以修改, 但很少修改
- 数据项 Ausprägung, Datenbank-Zustand
# 数据模型类型
- 关系型数据库: 表
- 树型, 层次型
- 网型
- 面向对象型
- 纯的很少
- 对象关系型
- 现在有些关系型数据库允许复杂的对象存储
- NoSQL-database
- e.g.
- MongoDB, documentorient
- 图数据库
- KV数据库
- 通常用于运行时间高相关型应用
- 一致性监视常常受限
- e.g.
# 数据库与软件的连接
- 通过库
- API
- SQL语句通过参数传递
- e.g.
- OCI: Oracle Call Interface
- ODBC: Open Database Conectivity
- JDBC
- 嵌入到语言
- C, C++
- SQLJ/JSQL for Java
e.g. SQLJ

- 由预编译器调用API
# 数据库的结构
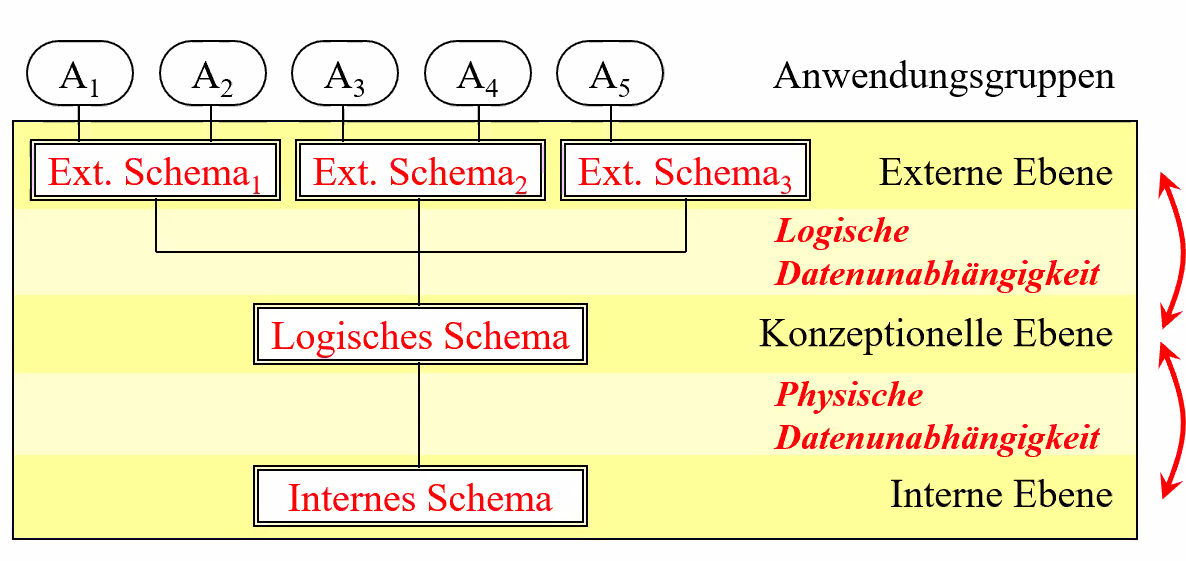
# Konzeptionelle Ebene
- 独立于单个数据库的, 所有数据的视图
- 由DDL指定
- 没有数据细节
# Externe Ebene
- 用户应该看到的数据
- 界面层
# Interne Ebene
内部模式描述了系统特定的数据库对象(物理存储)的实现,例如
- 存储数据记录的结构
- 索引结构,如搜索树
- 内部模式极大地决定了整个 DBS 的性能表现 -应用程序不受内部模式变化的影响(物理数据独立性)。
# Logische Datenunabhängigkeit
Die Datenbank wird von die Änderungen und Erweiterungen des Anwenderschnittstellen abgekoppelt. 数据库与使用接口的变化和拓展脱钩.
# Physische Datenunabhängigkeit
Die Anwendungen sind von die Änderung des internen Schemas nicht betroffen. (数据库的)使用不受其内部模式变化影响.
# Das Relationale Modell
Domain Kartesische Produkt Relation Kardinalität
# Relation in der Mathematik
Attribute Spalte einer Tabelle
Grad/Stelligkeit k in $R \subseteq D_1 \times D_2 \times \\ … \\ \times\\ D_k$
Relation = Menge von Tupel
# Relation in DBS
Relation rAusprägnung eines Relaionen-Schemas.AttributeSpalte einer Tabelle- Position relative
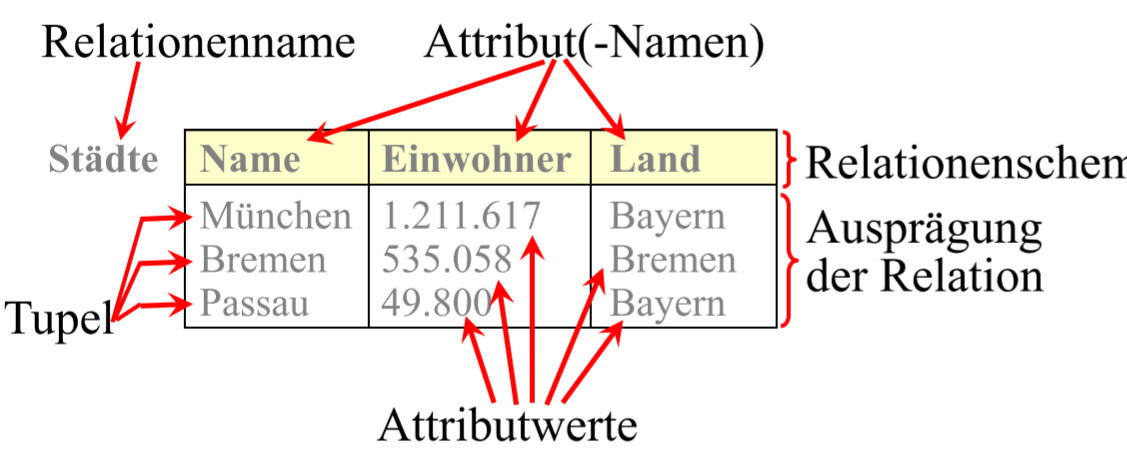
- geordnetes Relationschema
Attributnamen$A_i$, $R = (A_1\\ :\\ D_1,\\ …\\ A_k\\ :\\ D_k)$
- Relationenschema mit Domänenabbildung
dom(m)$R = {A_1,\\ …\\ A_k}, dom(A_i) = D_i, 1 \le i \le k$ 属性类型
- e.g.
 一行是一个项, 一个 关系的元素, 一个 tuple
一列是一个属性
一个关系是一张表
一行是一个项, 一个 关系的元素, 一个 tuple
一列是一个属性
一个关系是一张表
# Key
Key K 是 RelationenSchemas $R$ 的 Attribute 的子集 ($K\subseteq R$) 就是可以辨识唯一性的属性, 可以是一组属性或一个属性
Eindeutigkeit$\forall r,\\ t_1, t_2 \in r,\\ t_1 \neq t_2 \Rightarrow t_1[K] \neq t_2[K]$Minimalität$\forall T$ Attributmengen, die Eindeutigkeit erfüllen, $T \subseteq K \Rightarrow T = K$
# Superkey
Superschlüssel 满足 Eindeutigkeit, 而不一定 Minimalität (这意味着超钥也可以作为唯一辨识, 而且不一定所有属性都需要用上) Key 是 minimal Superkey
# Unique
Schlüsselkandidate unique 约束 符合 key, 即可作为唯一辨识符的一个或一组属性, 作为(数据表的 primary key)候选
# Primary key
从候选里选出的主键 符合 not null 约束
# Foreign key
一个表中的 foreign key 指向另一个表的 unique key
# Referential Integrity
通过外键连接起来的行的完整性 含有外键的行的完整性也包括引用的行的完整性
# SQL
# Die Relationale Algebra
# Relationale Algebra
Linear Algebra Concepts 线性代数概念
Linear Algebra Concepts 线性代数概念
# Relationale Algebra
- Operanden: Relationen(Tabelle)
- Operatoren: Selektoren(value>1000), UNION
- Abgeschlossenheit: Ergibnisse immer eine Relation
# Grundoperationen
- Vereinigung
- Differenz
- Kartesisches Produdt(Kreuzprodukt)
- Selektion
- Projekt
- (Umbenennung der Element)
# Projektion
删除不需要的列 e.g. $\pi_{Name,Abteilung}(Mitarbeiter)=…$
| Name | Abteilung |
|---|---|
| Huber | 01 |
| Mayer | 01 |
| Müller | 02 |
| Mayer | 01 |
# Operation
# Duplicate-Elimination
- $n\\ log(n)$
- sort
# Durchschnitt
$A \cap B = A - (A - B)$
- abgeleitete Operation
- 有时候被定义为 Grundoperation, 而 $-$ 是 abgeleitete
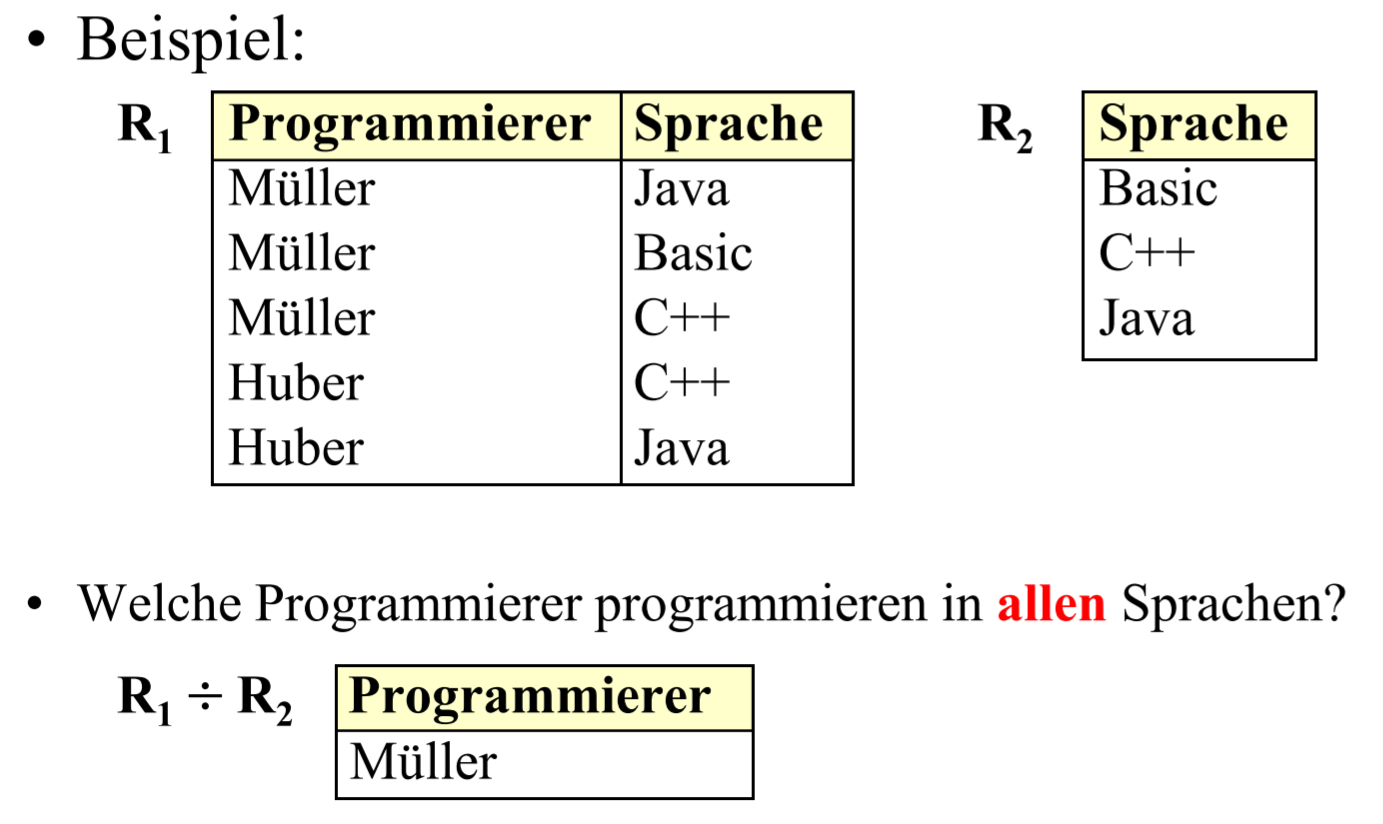
# Quotient
有一点 $\forall$ 的意思, $R_1 \div R_2$, $R_1$ 中只有完整包含 $R_2$ 中每一个项的项才被保留
# JOIN
Selektion+Kreuzprodukt e.g. $\sigma_{Ableitung=ANr}(Mitarbeiter \times Abteilung)$
| PNr | Name | Vorname | Abteilung | ANr | Abteilungsname |
|---|---|---|---|---|---|
| 001 | Huber | Erwin | 01 | 01 | Buchhandlung |
| 002 | Mayer | Hugo | 01 | 01 | Buchhaltung |
| 003 | Müller | Anton | 02 | 02 | Produktion |
符号 $R\\ \bowtie\\ S$
分类:
- Theta-Join(Selector) $R \underset{A\\ \Theta\\ B}{\bowtie} S$
- Equi-Join $R \underset{A=B}{\bowtie} S$
- Natural-Join 同名的 Attribute 会合并
# SQL & relational operators
SQL is relational complete
SELECT - projector SELECT 但不会删除相同的项, 需要 SELECT DISTINCT
FROM - crossproduct 通配符*, as
SELECT m.*, a.Name AS Abteilungsname, … FROM Mitarbeiter m, Abteilung a
可以 self-join, 即 FROM 两次自己,可以在将整个数据表与某一项的某一值比较时用
WHERE - selector
compare oprater: <=, <>, …
可以有 Prädikat: 加减乘除,concatenation ||, substring, 逻辑运算
inexact: A1 LIKE ‘Datenbank%‘ % 任意个任意字符 _ 一个任意字符
IN: A1 in (2, 3, 5, 6)
# Kompatible Wertebereich
# UNION, INTERSECT, EXCEPT, MINUS
UNION - with duplication UNION ALL - without duplication UNION CORRESPONDING - same attribute name only INTERSECT - intersection EXCEPT, MINUS - difference
UNION 支持不同属性名合并, 也可以用 NULL 作占位符 e.g.
SELECT A,B,C FROM R UNION SELECT A,D,C FROM S
# UPDATE
UPDATE relation SET a1 = v1 WHERE con
# DELETE
DELETE FROM relation WHERE con
# INSERT
将一个表或表的某些列复制到另一个表
INSERT INTO table2 (column_name(s))
SELECT column_name(s) FROM table1;
# Relationen Kalkül
# Relationen Kalkül
- deklarative Sprache, vgl. Relationale Algebra ist prozedurale Sprache
- Tupelkalkül & Bereichskalkül
# Tupelkalkül
| Syntax | Interpretation-> | Semantik |
|---|---|---|
| Tupelvariablen | -> | konkrete Tupel |
| Formeln | -> | true/false |
| Ausdruck | -> | Relation |
# Tuplevariablen
- kann in einer Formel frei oder gebunden auftreten
- haben Schemas
- $Schema(t) = (A_1: D_1, A_2: D_2)$
# Atom
- $R(t)$
- $t.A \\ \Theta \\ s.B$
- $t.A \\ \Theta \\ c$, c constant
# Formel
$\neg \wedge \vee \\ \forall \\ \exists$ von Atom
$I(\psi)$ Interpretation von Formel e.g. I(R(r)) = true
# Ausdruck(Anfrage)
${t | \psi(t)}$
ψ(r | t)
t Tuplevariable mit Schema(t)
r konkrete Tuple
ψ(r | t): alle t durch r ersetzt
e.g.


# Bereichkalkül
# Sicher(Ausdruck)
Tuplevariable 只能用 gespeicherten Relation 可接受的值, 即 positiv in einem Atom R(t) vorkommt
# Bereichvariablen
$x_1: D_1, \\ x_2: D_2$
# Ausdruck
${x_1, \\ x_2, \\ … | \psi (x_1,\\ x_2\\ …)}$
# Atom
- $R_1(x_1,\\ x_2,\\ …)$
- $x\\ \Theta \\ y$
# Formel
analog. Tupelkalkül Formel

# 某作业
${Nummer,Datum | \exists abt, art, lie:Verkauf(Nummer, Datum, abt, art, _, _, _)$ $\wedge Abteilung(abt, _, _, 3, _) \wedge Artikel(art, _, _, _, _, lie)$ $\wedge Lieferant(lie, _, _, Land)$ $\wedge (Land=Italien \vee Land=Frankreich)}$
c) $Schema(t) = Schema(Nummer: Integer, Name: String, Abteilung: String)$ ${[t.Nummer, t.Name, t.Abteilung]|$ $(\exists u \in Angestellter)(u.Nummer=t.Nummer \wedge u.Name=t.Name \wedge$ $(\exists v \in Abteilung)(v.Nummer=u.Abteilung \wedge v.Name=t.Abteilung \wedge$ $(\exists w \in Filiale)(w.Nummer=v.Filiale \wedge w.Stadt=Koeln)))}$
${nr, name, abt|\exists abtnr, filnr: Angestellter(nr, name, _, abtnr, _, _) \wedge$ $Abteitung(abtnr, abt, filnr, _, _) \wedge Filiale(filnr, Koeln, _) }$
d) $Schema(t) = Schema(Angestellter)$ ${[t.Nummer, t.Name, t.Gehalt, t.Geburtsjahr]|(t \in Angestellter) \wedge$ $(\exists v \in Verkauf)(v.Angestellter=t.Nummer \wedge v.Datum>01.10.2019) \wedge$ $(\neg \exists u \in Abteilung)(u.Leiter=t.Nummer)}$
${nr, name, gehalt, geburtsjahr|$ $Angestellter(nr, name,gehalt, abtnr, geburtsjahr, _) \wedge$ $\exists datum:Verkauf(_, datum, _, _, nr, _) \wedge$ $\neg \exists abtnr:Abteilung(abtnr, _, _, _, nr)}$
e) $Schema(t) = Schema(Lieferant)$ ${[t.Nummer, t.Name] |t \in Lieferant \wedge$ $(\exists art1, art2, art3 \in Artikel)(art1.Lieferant=t.Nummer \wedge$ $art2.Lieferant=t.Nummer \wedge art3.Lieferant=t.Nummer \wedge$ $art1 \neq art2 \wedge art1 \neq art3 \wedge art2 \neq art3)}$
${nr, name| Lieferant(nr, name, _, _) \wedge \exists art1, art2, art3:$ $Artikel(art1, _, _, _, _, nr) \wedge Artikel(art2, _, _, _, _, nr) \wedge$ $Artikel(art3, _, _, _, _, nr)\wedge art1 \neq art2 \wedge art1 \neq art3 \wedge art2 \neq art3)}$
a) $Schema(t) = Schema(R)$ ${t|t \in R \wedge t.A=x}$
${a, b, c|R(a, b, c) \wedge a=x}$
b) $Schema(t) = Schema(R)$ ${[t.A, t.B]|t \in R }$
${a, b|R(a, b, _)}$
c) $Schema(t) = Schema(A, B, C, D, E$) ${t|(R.C=S.C \wedge R.A=t.A \wedge$ $R.B=t.B \wedge S.D=t.D \wedge S.E=t.E)}$
${a, b, c, d, e| R(a, b, c) \wedge S(c, d, e)}$
d) $Schema(t) = Schema(R)$ ${t|t \in R \vee t \in S}$
${a, b| R(a, b, c) \vee S(a, b, c)}$
e) $Schema(t) = Schema(R)$ ${t|t \in R \wedge t \in S}$
${a, b| R(a, b, c) \wedge S(a, b, c)}$
f) $Schema(t) = Schema(R)$ ${t|t \in R \wedge t \notin S}$
${a, b| R(a, b, c) \wedge \neg S(a, b, c)}$
g) $Schema(t) = Schema(A, B, C, D, E, F)$ ${t|t.A=R.A \wedge t.B=R.B \wedge t.C=R.C \wedge t.D=S.D \wedge t.E=S.E \wedge t.F=S.F}$
${a, b, c, d, e, f|R(a, b, c) \wedge S(d, e, f)}$
h) $Schema(t) = Schema(B)$ ${t|(\forall s \in S)((\exists r \in R)(R.A=S.A \wedge r.B=t.B))}$
${b|\forall a: S(a) \\ \exists r: R(a, b)}$
# Query By Example (QBE)
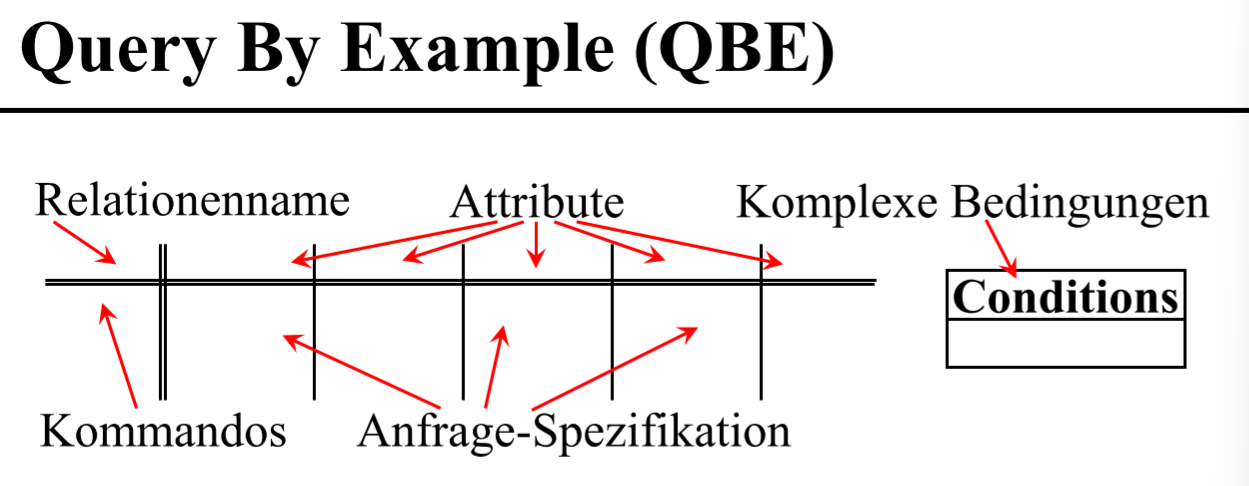
- Kommandos
P.print/projektionI.insertD.deleteU.update
- Bereichsvariablen
- _x, _y
- Konstanten
- Operator
- Condition-Box
- AND, OR, but no NOT
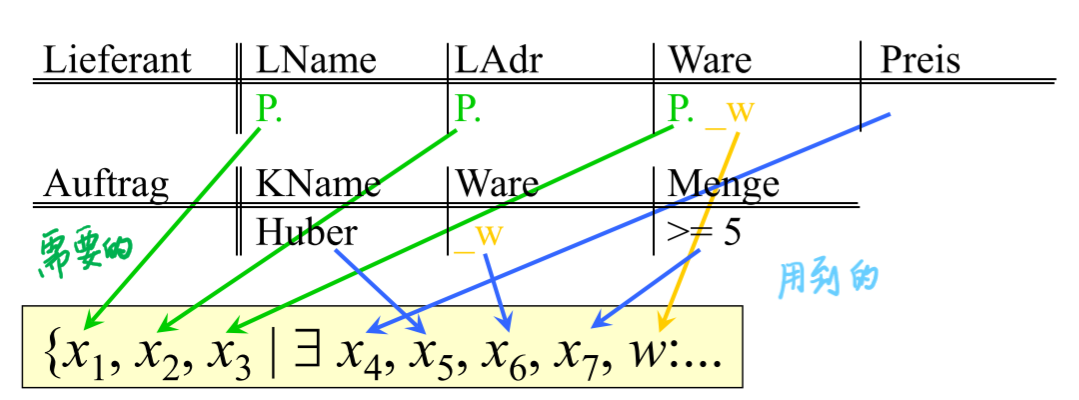
# Umsezung von Bereichkalkül zu QBE Anfrage


# Quantoren und Subqueries in SQL
${x \in R\\ |\\ \exists y \in S: con} \equiv \pi_{R.^*}(\sigma_{con} (R \times S))$ ${x \in R\\ |\\ \forall y \in S: con} \equiv (\sigma_{con} (R \times S)) \div S$
${x \in R\\ |\\ \forall y \in S: x.a > y.b} \equiv (\sigma_{x.a>y.b} (R \times S)) \div S$
# Sortieren, Gruppieren und Views in SQL
# Sortieren
# Aggregation
# Gruppierung
# Auswertung
# Das E/R Modell
Entity/Relationship Model
-
Entity: class, 两个 Entity 之间只能通过 Relationship 连接
-
Attribute
-
Relationship: e.g. belegt(Anton, dbs) 关系也是可以有属性的
-
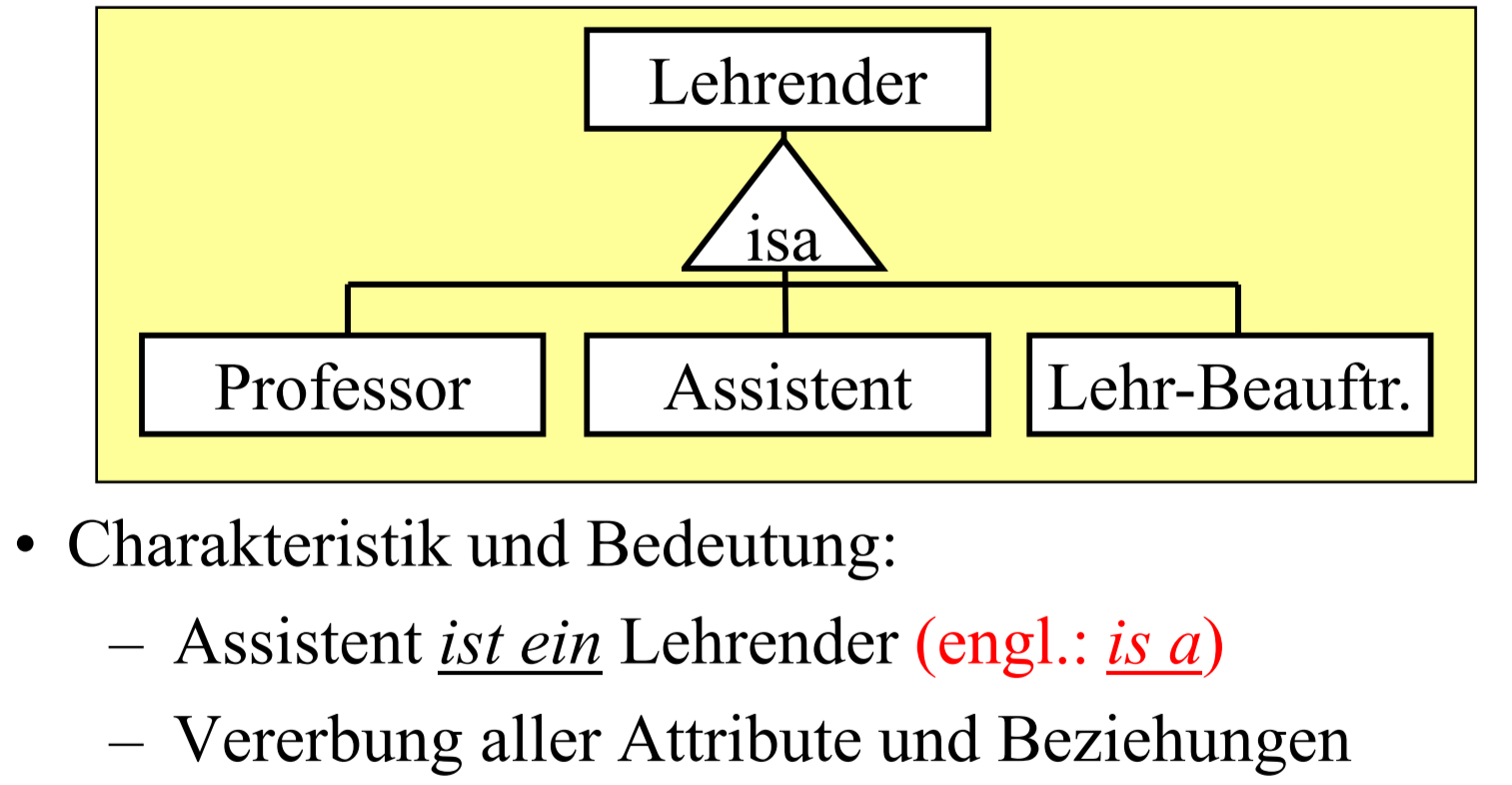
(erweiterte) Vererbung
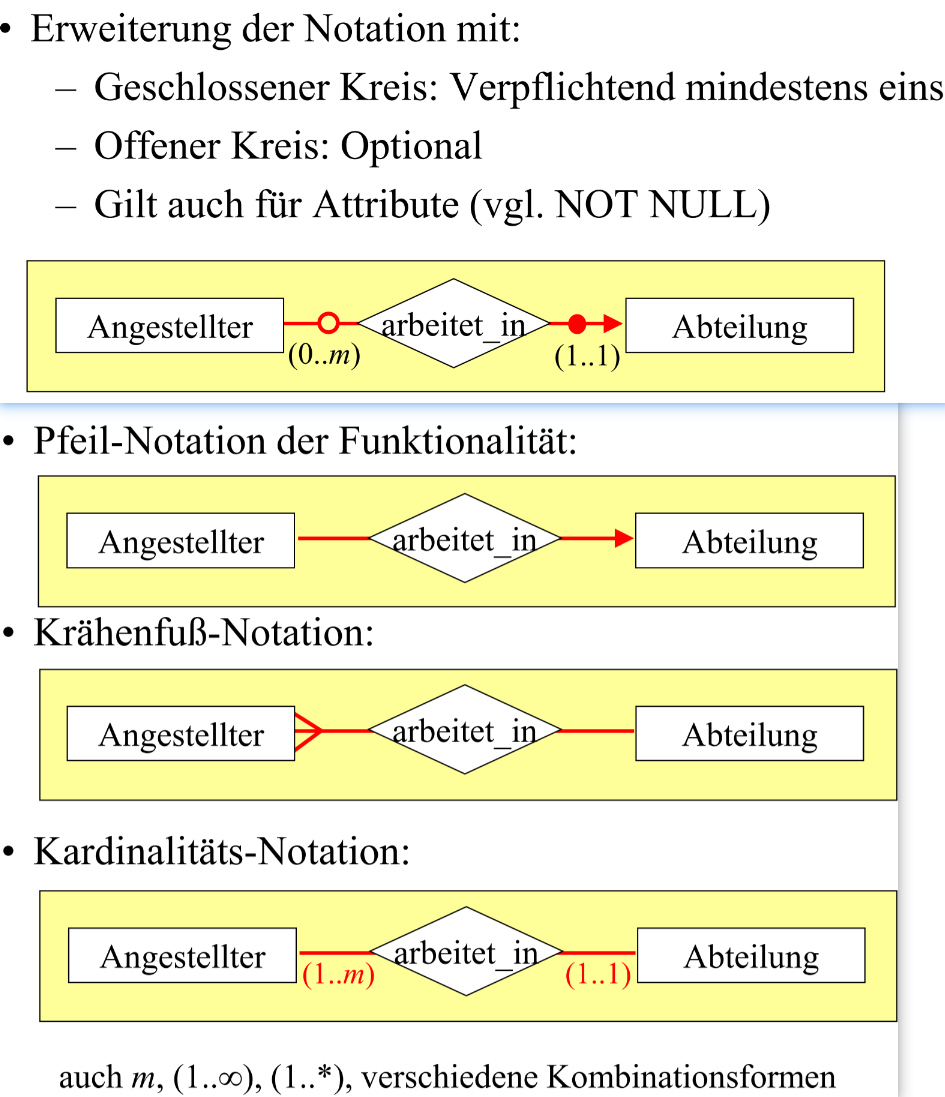
# Notation
- 1:1(双箭头)
- m:1(多指向1)
- m:n(无箭头)
Vererbung
# E/R 转 Relation
# 1:1
如果合理的话, 两个实体合为一个
# 1:n
将 1 的主键加入到 n 作为外键
# m:n
将 关系 作为新的表, 将关系双方的主键作为外键且是新的表的主键
# 多方关系
也是创建新的表, 将关联的表的主键作外键+主键
# 同类关联
按照上面的规则, 属性改个名字就好
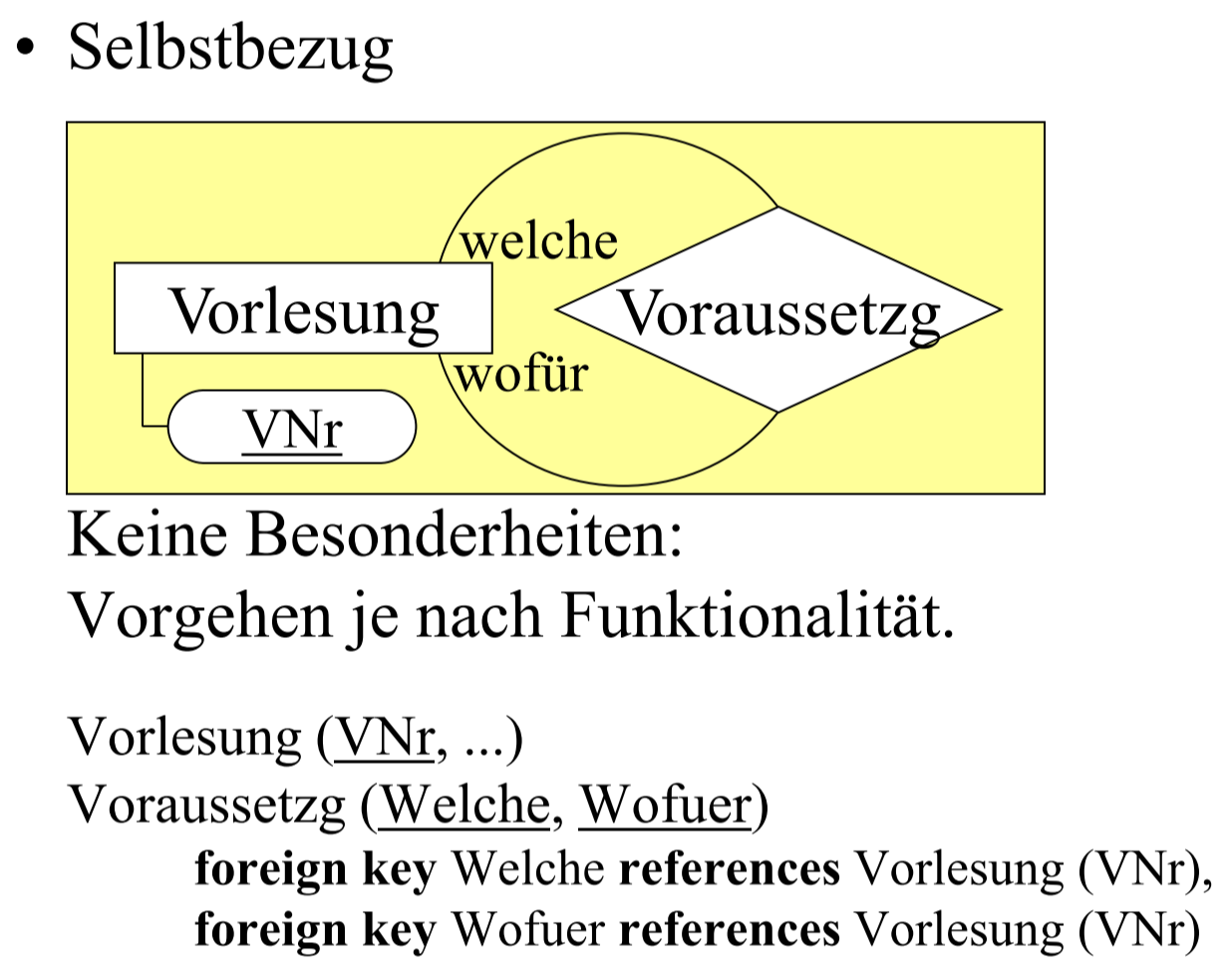
# 继承
通常可以转化为 1:m 也可以直接将父类的属性加入到子类, 取消父类
# UML
类似类图
- 关系没有特殊符号, 直接标注在线上, 只有三元+关系用菱形
- ..
# 某作业
(提示: 这不是E/R图, 我做错了)
# Normalformen
Normalization theory as formal basis for RDB design.


# 概念
# Functional dependency
同一个表中的属性之间的依赖 (X -> Y) Y ist von X funktional abhängig
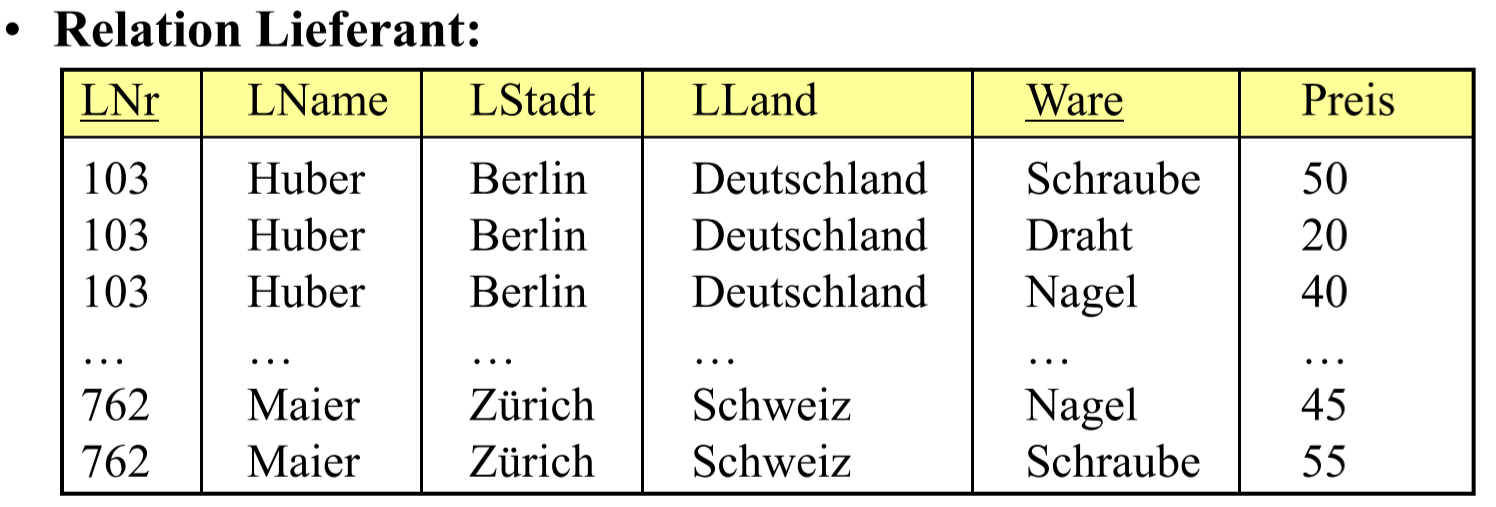 是指比如说, 在一个设计不当的表中, 某几个属性与某主键挂钩, 某几个与另一个属性挂钩(不一定是主键, 如LStadt和LLand)的情况, 这样就会造成冗余(Redundanz).
这种情况就很容易造成:只更新了其中一项的内容
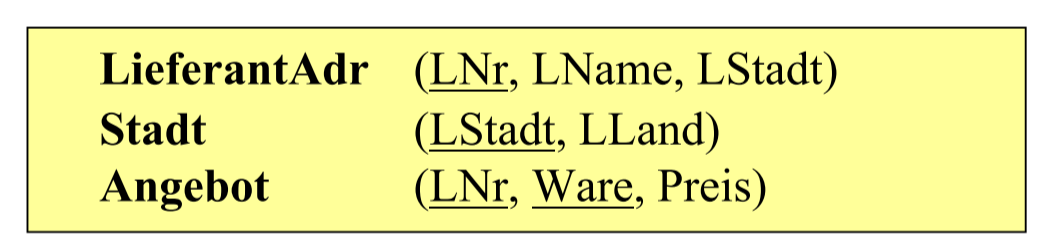
更改成更好的 Schema:
是指比如说, 在一个设计不当的表中, 某几个属性与某主键挂钩, 某几个与另一个属性挂钩(不一定是主键, 如LStadt和LLand)的情况, 这样就会造成冗余(Redundanz).
这种情况就很容易造成:只更新了其中一项的内容
更改成更好的 Schema:
# 更改异常(Update-Anomalie)
指由于同一数据的重复存储, 修改一处必须找出其他多处
# Partielle FD, Volle FD
已知 $X \rightarrow Y$,
- 若没有有 $X^{\prime} \subsetneqq X$ 且 $X^{\prime} \rightarrow Y$, 则称 $X \rightarrow Y$ volle FD($X \overset{\bullet}{\rightarrow} Y$)
- 否则是 partielle FD
volle 相当于最小化了, 这个就是可以提取成新表的主键 partielle 意味着还得找 volle
# Full FD vs. Key
Key 不一定代表其他属性就对它 full FD, 因为 ffd 是一个集之间的关系, $X$ 是 key vs. $X \rightarrow Y$, 前者代表 X 可以确定一个项(的其他属性作为一个整体), 后者代表可以确定 Y 中的每一个属性. 前X和后X在一张表里可能不相等, 如果相等说明设计得好
# Triviale funktionale Abhängigkeit
由于 , 每个属性对自己和包含自己的集 FD 这种关系称为 trivial funktionale Abhängigkeit.
# Prime Attribute
Ein Attribut heißt prim, wenn es Teil eines Schlüsselkandidaten ist
# verlustlos/verbundtreu
指一张表分离成两张时无损, 即 $R = R_1 \bowtie R_2$ 这通常需要 $R_1$ 和 $R_2$ 的交集等价于两者之一 (这个等价也包括外键带来的数据)
# abhängigkeitserhaltend/hüllentreu
描述一张表分离成两张时保持 functional dependency 状态 需要 $F_R = (F_{R_1} \cup F_{R_2})$ bzw. $F_R^+ = (F_{R_1} \cup F_{R_2})^+$ $F_R$ functional dependency of Relation R
# Hülle einer Attributmenge
属性集的凸包 F: Set of FDs X: Set of Attributes res = $X^+$: vollständige Menge von Attributen $X^+$, fürdie gilt $X \rightarrow X^+$
|
|
# Notation Convention
Attribute: A, B, C Attribute set: X, Y, Z
看起来就是为了functional dependency简化的 Notation表

# Herleitung von FD
# Axiome

# Reflexitivity(R)
$Y$ 是 $X$ 的子集, 则恒有 $X \rightarrow Y$ $X \rightarrow X$ 恒成立
# Verstärkung(VS)
若 $X \rightarrow Y$, 则 $XZ \rightarrow YZ$ $XZ = X \cup Z$
# Transitivity(T)
$X \rightarrow Y$ 且 $Y \rightarrow Z$, 则 $X \rightarrow Z$
# 显然FD没有对称性
# Vereinigungsregel(VE)
$X \rightarrow Y$ 且 $Y \rightarrow Z$, 则 $X \rightarrow YZ$
# Dekompositionsregel(D)
$X \rightarrow YZ$ 则 $X \rightarrow Y$ 且 $X \rightarrow Z$
# Pseudotransitivitätsregel(P)
$X \rightarrow Y$ 且 $YZ \rightarrow V$, 则 $XZ \rightarrow V$
# 证明 key candidate



# 1. Normalform
FNF, first normal form
Def. Ein Relationenschema ist in 1. Normalform, wenn alle Attributwerte atomar sind 只要每个属性只有一个值就是
“nested relation”, non first normal form, NFNF, NF2 e.g. group by In SQL nur temporär erlaubt
# 2. Normalform
Motivation 避免有多键的表中, 属性只对其中一键依赖的情况
Def. Ein Schema ist in 2. Normalform, wenn jedes Attribut
- voll funktional abhängig von allen Schlüsselkandidaten
- oder prim ist verletzt: existiert zusammengesetzter Key(candidate) $\wedge$ existiert nicht prime Attr
# Zur 2.Normalform
将导致 pfD 的部分单独提取成一张表, 被依赖者为 key, 依赖者为属性
e.g. Lieferant(LNr, LName, LStadt, LLand, Ware, Preis) ↓ Lieferung(LNr, Ware, Preis) LieferAdr(LNr, LName, LStadt, LLand)
# 3. Normalform
Motivation 避免对非 key 属性的依赖
Def. Ein Relationenschema ist in 3. Normalform, wenn für jede nicht triviale funktionale Abhängigkeit $X \rightarrow A$ gilt:
- X 包含 key candidate oder
- A ist prim 2.N 的要求已经隐式包含
就比如说 如果一个属性 B 依赖于另一个属性 A, 那就是非 trivial 如果这个 A 还是个非 key candidate属性, B 也不是 prim, 那就违反了 3.N 的要求
# Zur 3. Normalform
将 依赖非key 的部分(或者说传递性依赖)单独提取成一张表, 被依赖者为 key, 依赖者为属性
# Synthesealgorithmus für 3NF
Idea 拆表, 合理设计数据库
Input
- Relation $R$
- $F$ FD von R
Output
- $R_1, \\ …, \\ R_n$ verlustlose, abhängigkeitserhaltende Zerlegung von $R$ in 3NF
Algorithm
- 确定 $F$ 的最简形式 $F_c$ (kanonische Überdeckung)
对所有 FD $X \rightarrow Y$:
- 检查所有 $A \in X$, A 是否多余, 即$Y \subseteq AttrHull(F, X - A)$ 是否成立. 若是, 则改为 $(X-A) \rightarrow Y$.
- 检查所有 $B \in Y$, B 是否多余, 即 $B \subseteq AttrHull((F-(X \rightarrow Y)) \cup (X \rightarrow(Y-B)), X)$ 是否成立. 若是, 则改为 $X \rightarrow (Y-B)$.
- 去除 $X \rightarrow {}$.
- 合并 $X \rightarrow Y_1,\\ …,\\ X \rightarrow Y_n$ 为 $X \rightarrow (Y_1 \\ \cup \\ … \\ \cup \\ Y_n)$.
- 从 $F_c$ 创建新的 Relationenschemata
对所有 $X \rightarrow Y \in F_c$:- 新 schema $R_X := X \cup Y$
- 分配 FD, $F_X := {X’ \rightarrow Y’ \in F_c | X’ \cup Y’ \in R_X}$
- 重设大表的 key candidates
- 删除多余关系


# 某作业
{ C, A → D ; C → F, D ; B → A, E ; E → F, A }
1.
a)
Linksreduktion:
C, A -> D
{C} $\subseteq$ AttrHülle(F, {C, A} - {A})
weil C -> F, D direkt gilt
b)
Rechtsreduktion:
C -> D
{C} $\subseteq$ AttrHülle(F - (C->D) $\cup$ (C->{}), {C})
weil es C -> F, D schon gibt
B -> A, E
{A} $\subseteq$ AttrHülle(F - (B->A,E) $\cup$ (B->E), {B})
weil B -> E und E -> A (transitiv)
c) C -> {} wird eliminiert
d) nichts zu tun
Fc = { C -> F,D ; B -> E ; E -> F,A}
R1(C, F, D) {C -> F, D} R2(B, E) {B -> E} R3(E, A, F) {E -> A, F}
R(B, C) weil (B,C) Schlüsselkandidate ist (10-5 (a))
nichts zu tun
# 3NF 还有什么问题?
还有这样的属性被依赖: prim, 但不能只凭自身构成 key candidate 的属性.

# Boyce-Codd Normalform
Def. Ein Schema R ist in Boyce-Codd Normalform, wenn für alle nichttrivialen Abhängigkeiten $X \rightarrow Y$ gilt:
-
$X$ enthält einen Schlüsselkandidaten von R
-
velustlose Zerlegung möglich
-
abhängigkeitserhaltende Zerlegung nicht immer möglich
# Mehrwertige Abhängigkeiten(MVD)
- mehrere unabhängige 1:n Beziehungen in einer Relation stehen.
- $X \twoheadrightarrow Y$

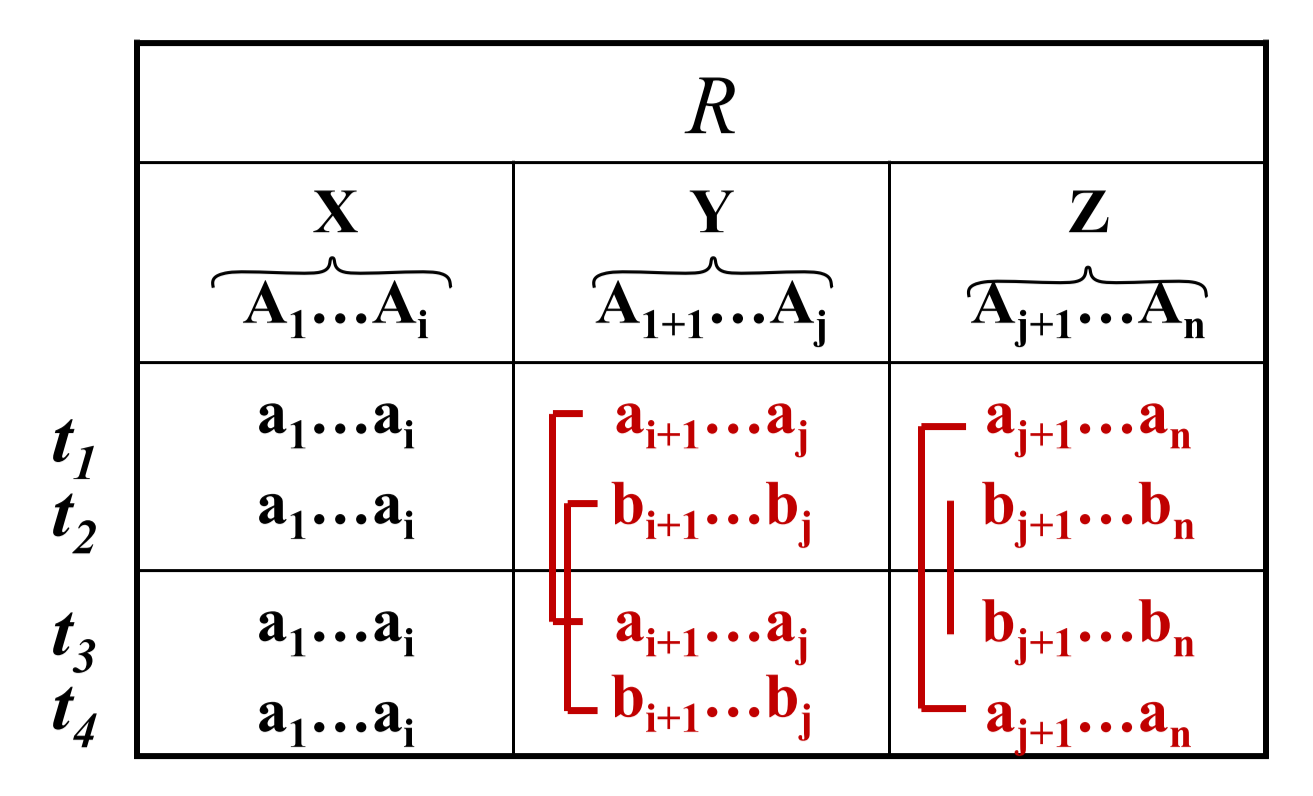
verlustlose Zerlegung von MVD, wenn gilt:
- $R = R_1 \cup R_2$
- $(R_1 \cap R_2 \twoheadrightarrow R_1) \vee (R_1 \cap R_2 \twoheadrightarrow R_2)$
# triviale MVD
Def. Eine MVD $X \twoheadrightarrow Y$ bezogen auf $R \supseteq X \cup Y$ ist trivial, wenn jede mögliche Ausprägung $r$ von $R$ diese MVD erfüllt, genau dann wenn:
- $(Y \supseteq X) \vee (Y = R-X)$
# 4. Normalform
Def. Eine Relation $R$ mit zugeordneter Menge $F$ von funktionalen und mehrwertigen Abhängigkeiten ist in 4. Normalform(4NF), wenn für jede MVD $X \twoheadrightarrow Y \in F^+$ eine der folgenden Bedingungen gilt:
- die MVD ist trivial
- oder X ist Superschlüssel von R
# Physische Datenorganisation
# 磁盘的结构和原理
- 一个
盘两面可读写 - 读写头可以在不同
轨道之间移动 - 轨道分成多个
扇区
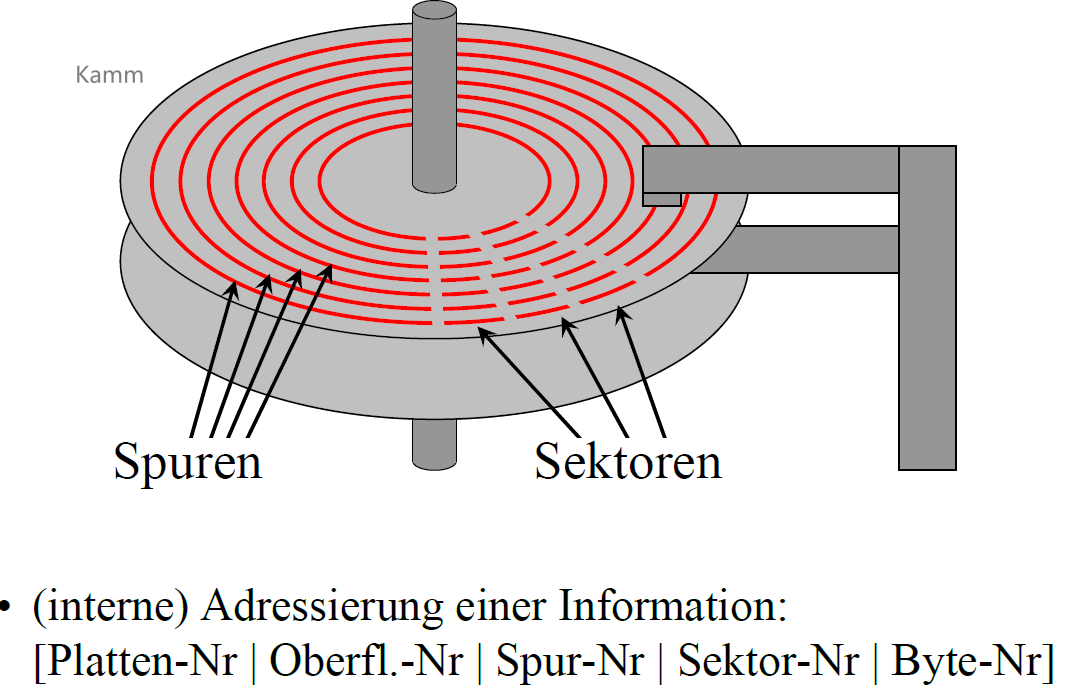
# 数据读取的速度
# Index 结构
Index 结构是数据的存储结构
# Index 结构
构造:
- Directoryseiten: index/directory
- Datenseiten: physische Datensätze
分类:
- Datenorganisierende Strukturen
- Raumorganisierende Strukturen
primary key search: B-Tree, 线性哈希 secondary key search: inverted list
# 数据库 Index 结构的要求
- 高效查找: 如果不优化, 难道一条一条数据找吗
- 动态插入, 删除和更改: 不可能改一下就要重新组织整个结构(如有序队列)
- 保持有序:如关联的数据应该在附近(局部性原理)
- 高存储利用率(Speicherplatzausnutzung)
# B 树
# B+ 树
# Hashing 方法
- Raumorganisierendes Verfahren
- 最好情况下读取时间复杂度可以到常数
# 二级存储的 Hash 方法
de. Hash-Verfahren für Sekundärspeicher
- 高存储利用率(50% Datenseiten)
- 高效的动态方法(插入, 删除, 更改)
- 查询的效率可以
# Hash 方法分类
- with directory
- without directory
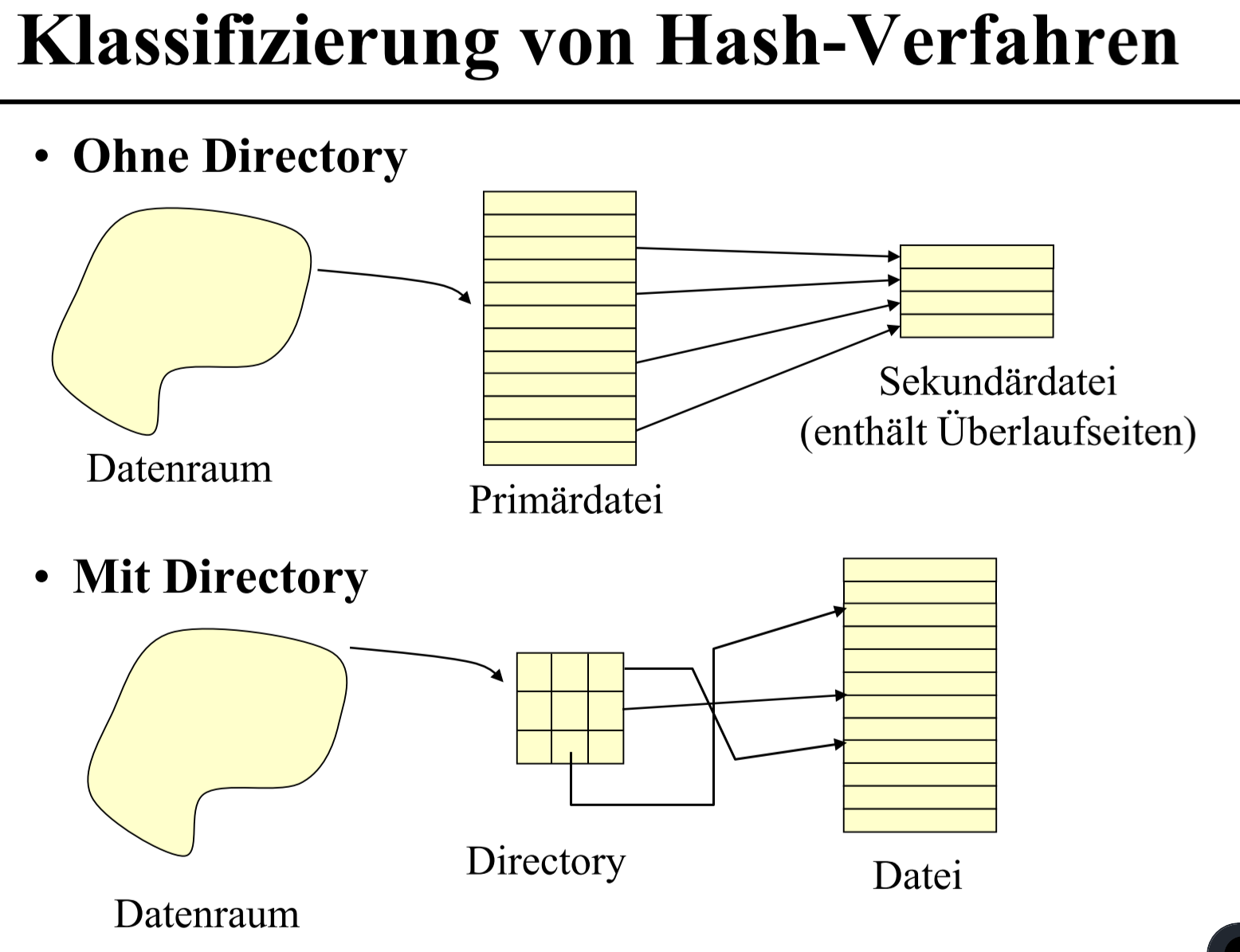
# Hash method with directory
- hash(k)/h(k) 计算结果是一个 bit 字符串, 也就是由 0和1 组成的数列
- depth d 是 bit 字符串位数, 一共有 $2^d-1$ 可用 bit串, 深度可变
- 出现撞表时, 如果不能分表, 则扩表
- 某一个数据占表比例太大(>90%)也会分表
- 不同的哈希值可能指向同一个数据, 通常是扩表导致的
# Linear Hashing
Hash method without directory
- hash() 直接计算得到存储地址
- 撞表 -> 把撞表地址关联
- 有一系列 hash function: $h_0, h_1,h_2,\\ …$
- 存储率 Belegungsfaktor 大于阈值 Schwellwert 会对溢出页使用下一个 hash function
- 存储空间使用随数据量线性增长
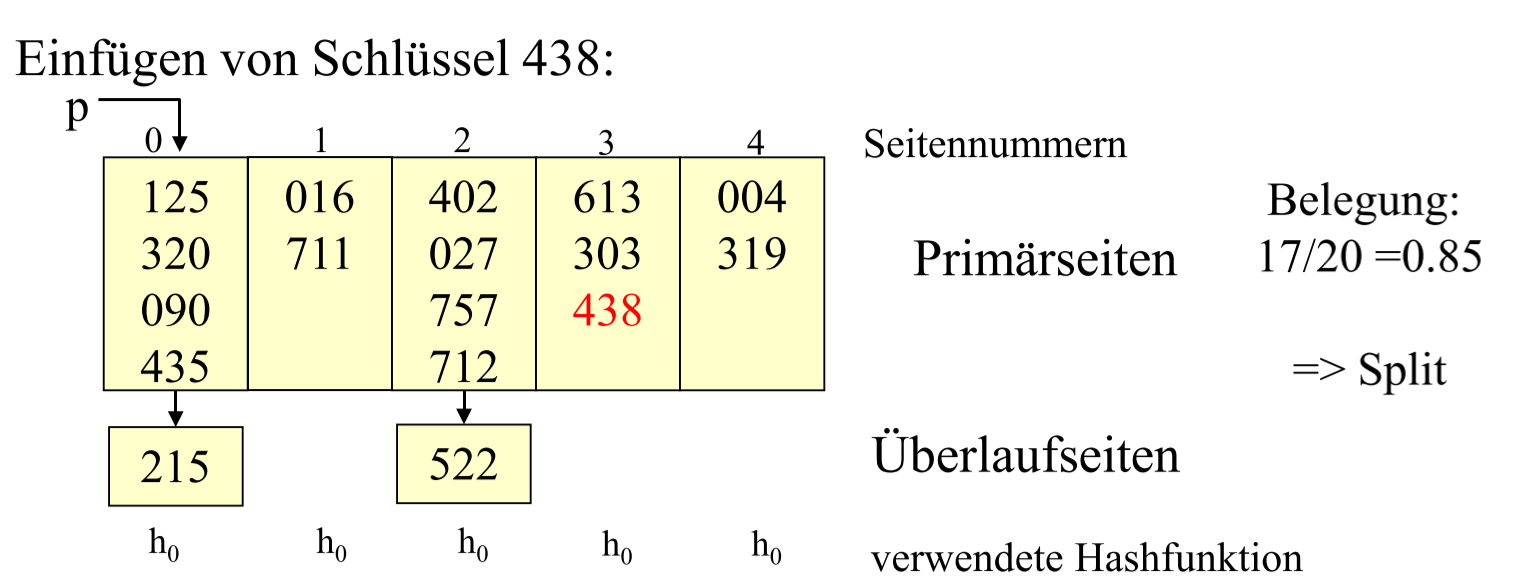
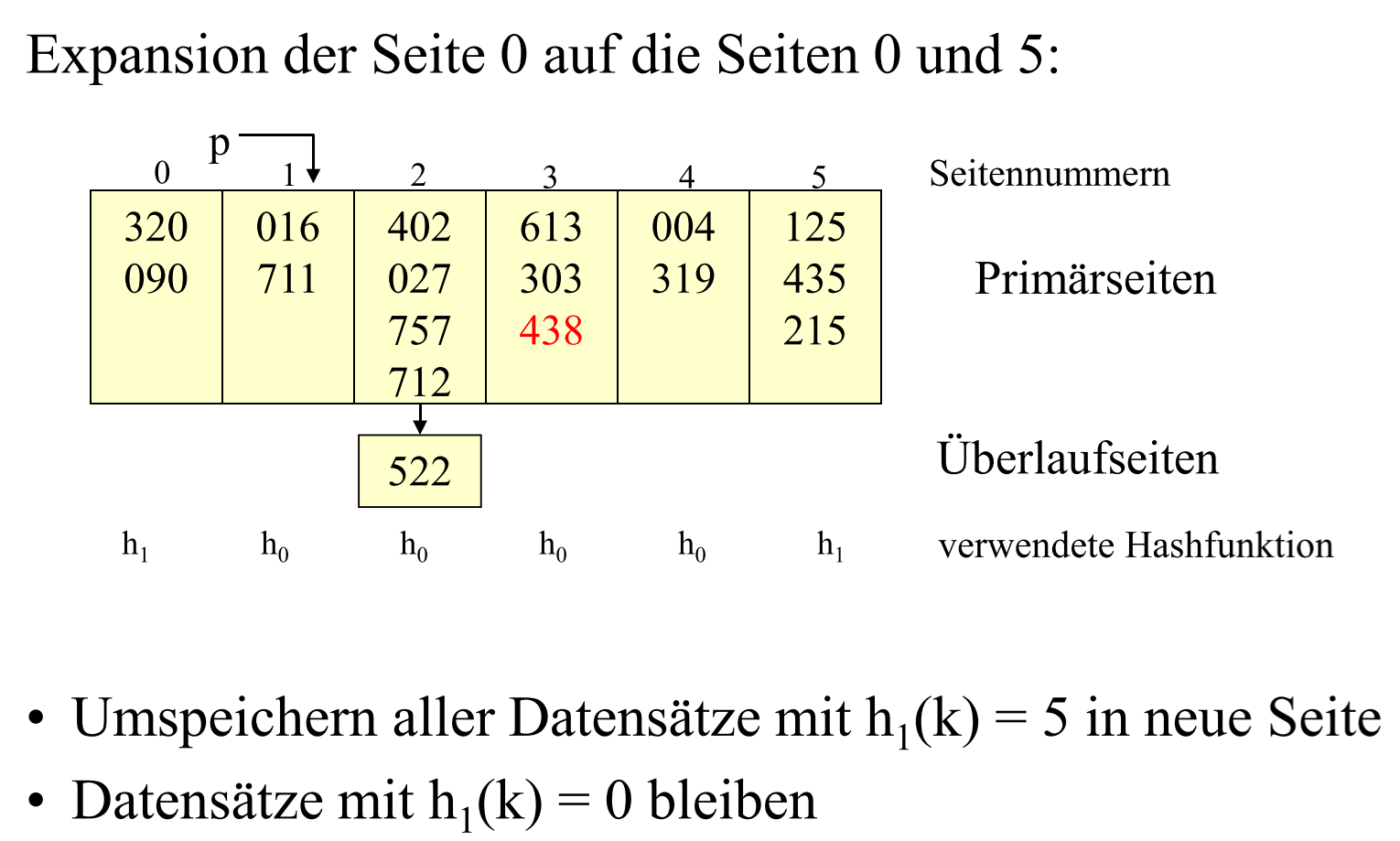
hash 方法是有要求的, 对第 L 个方法 $h_L$(从$h_0$开始):
- 对值域的要求: $h_L: domain(k) \rightarrow {0, 1, …, (2^L \times N) -1}$, 即第 L 个函数要保证值域中 #值=$2^L \times N$
- 对相邻函数的要求: $h_{L+1} = h_L(k) | h_L(k) + 2^L \times N$ e.g. $h_L(k) = k\mod (2^L \times N)$
# Inverted Index in DBS
- 对每个 attribute 的具体值 $a_1, a_2, …, a_d$ 建立反向索引
- Antwortzeit 不会随#回答数据增加
- Suchzeit 随#Attribute 增加
- 对非主键, 二级索引不会影响物理存储
# SQL 中的 Index
# Relationale Anfragebearbeitung
# Grundlage der Anfrageoptimierung
# Aufgabe der Anfragebearbeitung
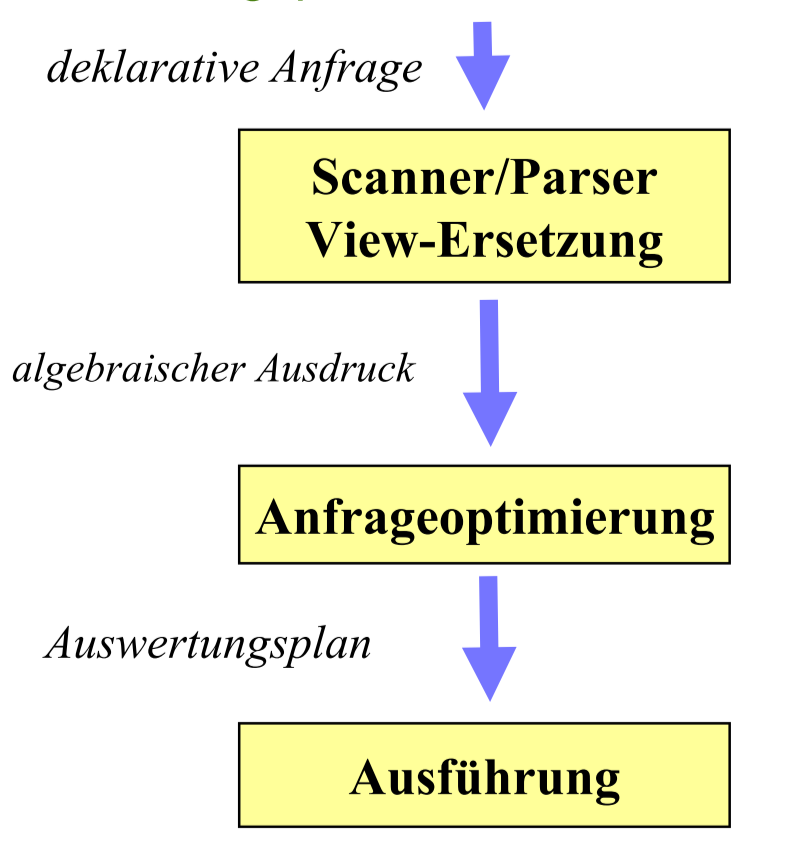
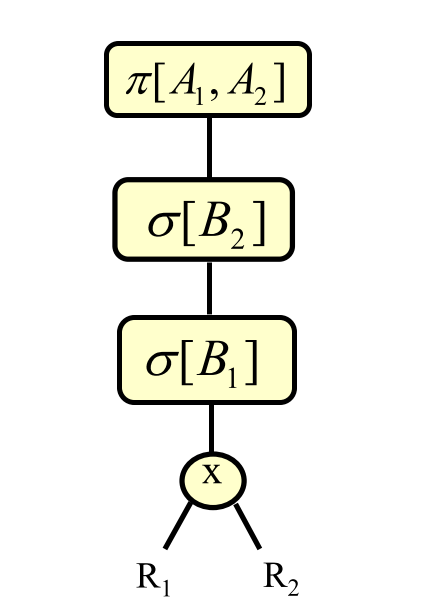
# Kanonischer Auswertungsplan
|
|
to $\pi_{A_1, A_2}(\sigma_{B_2}(\sigma_{B_1}(R_1 \times R_2)))$
- Produkt der Relationen
- Selektionen mit Bedingungen
- Projektion
# Logische vs. Physische Anfrageoptimierung
logische 的比如说改变 plan 子行为的顺序 physische 涉及到存储的使用策略
# Regelbasierte vs. Kostenbasierte Anfrageoptimierung
regelbasiert/algebraische 比如利用等价的规则来优化 kostenbasiert 就是先看成本再选择方案
# Logische Anfrageoptimierung
# Äquivalenzregeln der Relationalen Algebra
Commutative: join, union, intersect, crossproduct, selection* Assosiative: join, union, intersect, crossproduct, selection*
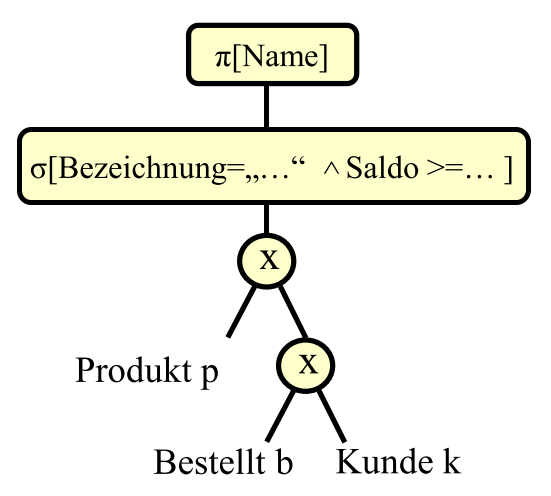
# Restrukturierungsalgorithmus
- 拆分(复数) selection 并尽可能在前面地执行 selection(比如在 product前, 减少 product 的数据量爆炸)
- select + cross -> join
- project 尽可能晚
- 将可以合并的 selection 合并
|
|
开始时的 Kanonischer Auswertungsplan
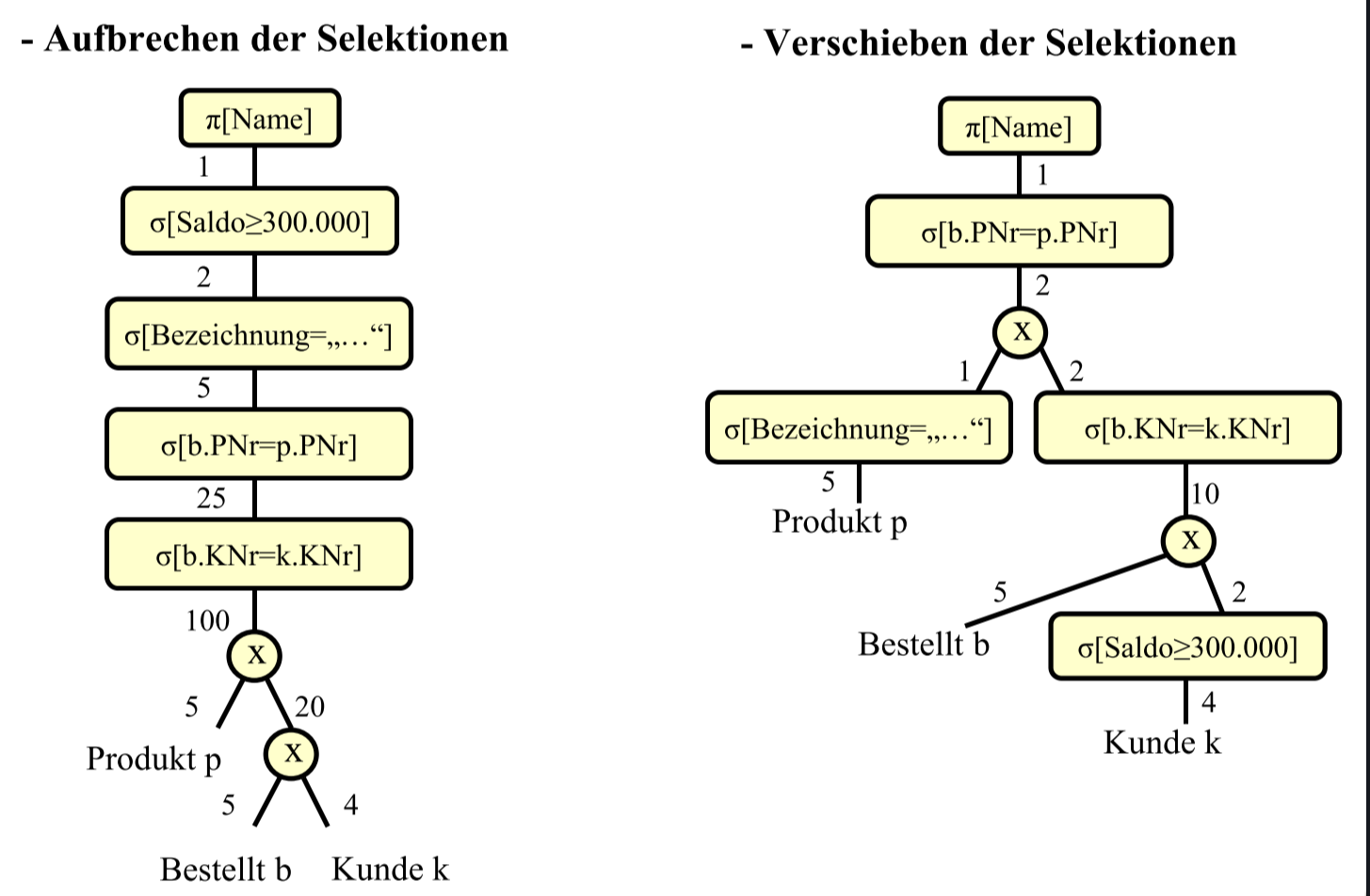
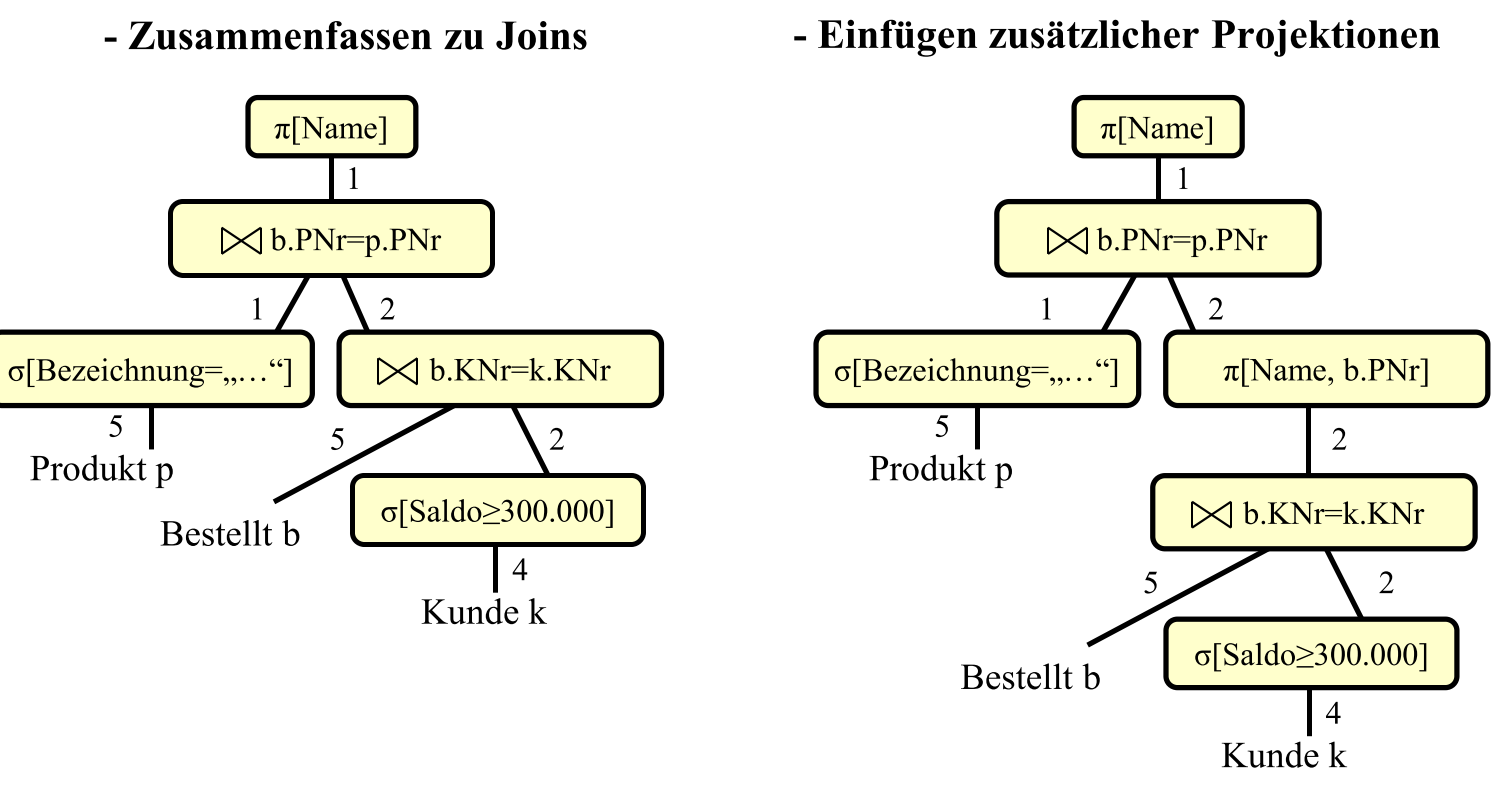
# Kostenmodellbasierte Anfrageoptimierung
# Selektivität
$sel$ 表示经过一个操作后剩下的条目比例
Selection $sel_B = \frac{\sigma_B(R)|}{|R|}$ Join $sel_{RS} = \frac{|R \bowtie S|}{|R \times S|} = \frac{|R \bowtie S|}{|R| \cdot |S|}$
AND: $sel_B(\sigma_{B1 \wedge B2}) = sel_B(\sigma_{B1}) \cdot sel_B(\sigma_{B2})$ OR: $sel_B(\sigma_{B1 \vee B2}) = sel_B(\sigma_{B1}) + sel_B(\sigma_{B2}) - sel_B(\sigma_{B1}) \cdot sel_B(\sigma_{B2})$ NOT: $sel_B(\sigma_{\neg B1}) = 1 - sel_B(\sigma_{B1})$
# Schätzmethoden
# Parametrische Verteilungen
对数据进行分布拟合
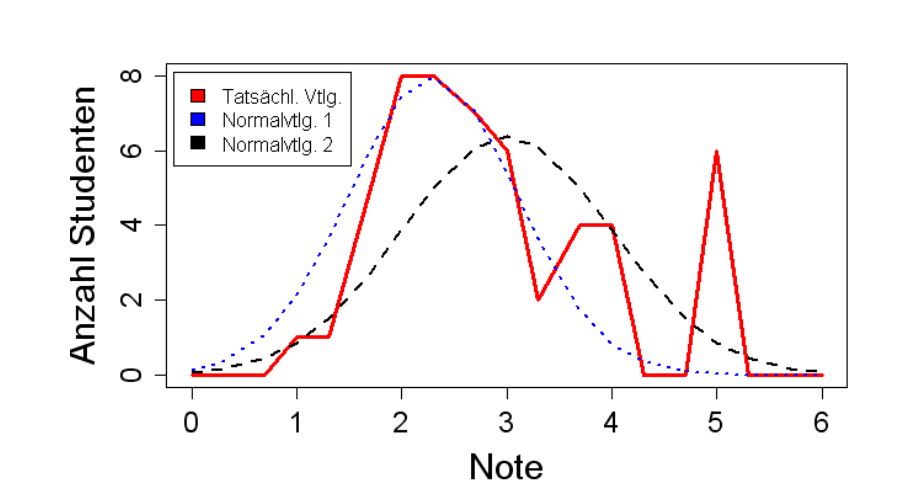 难点: 分布的选择, 分布参数的测定. 最大的问题是无法在多属性查询时使用
难点: 分布的选择, 分布参数的测定. 最大的问题是无法在多属性查询时使用
# Histogram
把数据划分为区间, 观察区间内数据分布情况 等宽直方图: 区间等宽 等深直方图: 每个区间的数据数量相同
一维直方图在多属性时的问题是, 假设了各属性间无关联 多维直方图在多属性时的问题是, 成本随维度指数增长000000000000000000000
# Stichproben
就是随机数, 蒙特卡罗方法, 难点在于 n 的选择, 太小不准, 太大又贵
# Physische Anfrageoptimierung
目的: 对某一次操作(例如查询)寻找最适合的算法和数据结构
R JOIN S ON R.A=S.B
# Notation
$BR/BS$:number of blocks $f_R/f_S:\\ \\ #relations/block$ c : size of cache (Bytes) $t_{tr}$ : transfer time $t_{lat}$ : 磁盘的平均延迟 b: size of block
其中 b 也就是 Block 大小是要被最优化的参数(现实一般好像是16kb)
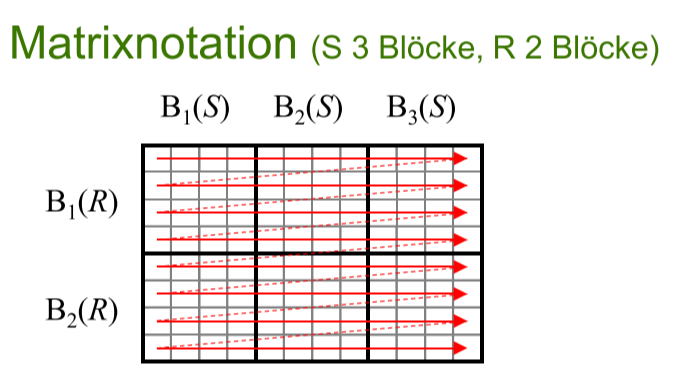
# Nested-Block-Loop-Join(NBL-Join)
- 每个小格子是一个数据项(的对比), 一个 Block 是4项, 4x4 是16次对比
# Einfacher Nested-Loop-Join
|
|
(Blockzugriffe) $#load = BR \times (f_R \times BS + 1)$
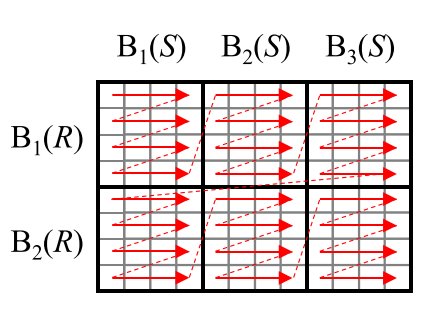
# Nested-Block-Loop-Join
- 稍微优化一点, 稍微优化 Block 读取次数, 着眼当前地充分利用每次 load block
|
|
$#load = BR \times (BS + 1)$
# Cache Strategy for NBL-Join
关键: size of block 太小了太大了都会增加读写次数
其一
在的基础上, 加入缓存机制, 并将 Block读取顺序 Z 形读取改为 蛇形(是整个Block的读取, 不是Block内部)
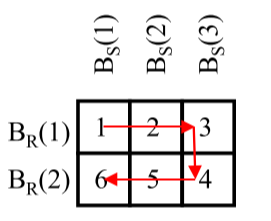
$|C|$ : 可用的 cache 能放多少 Block
Blockzugriffe = $BR + BR \cdot (BS - |C| + 1) + |C| -1$
其二 用 $|C|$ - 1 个 Page 缓存 R, 剩下那一个缓存 S
例如 $|C|$ = 3
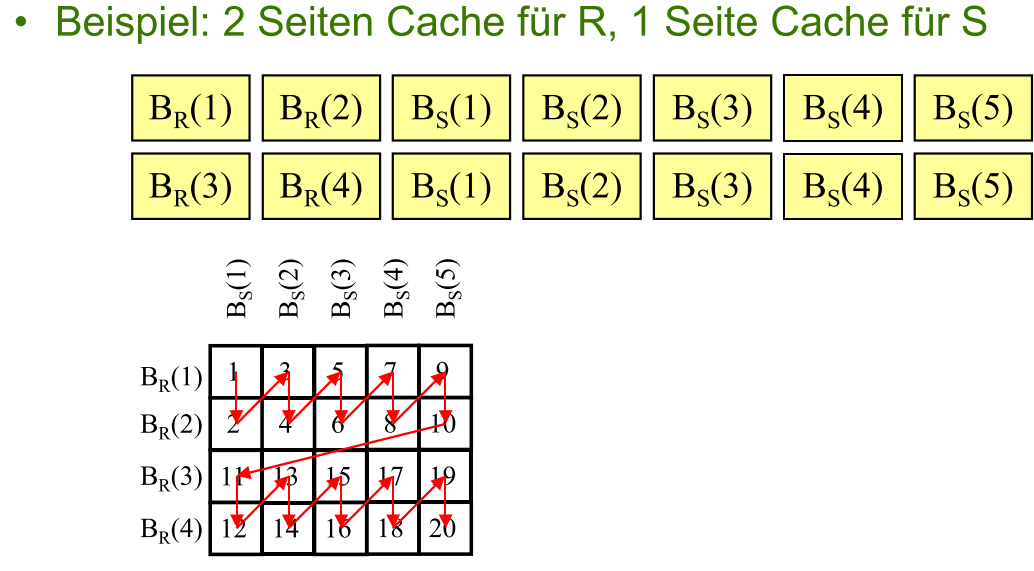
Blockzugriffe = $B_R + B_S \cdot \left \lceil \frac{B_R}{|C|-1} \right \rceil$
I/O用时
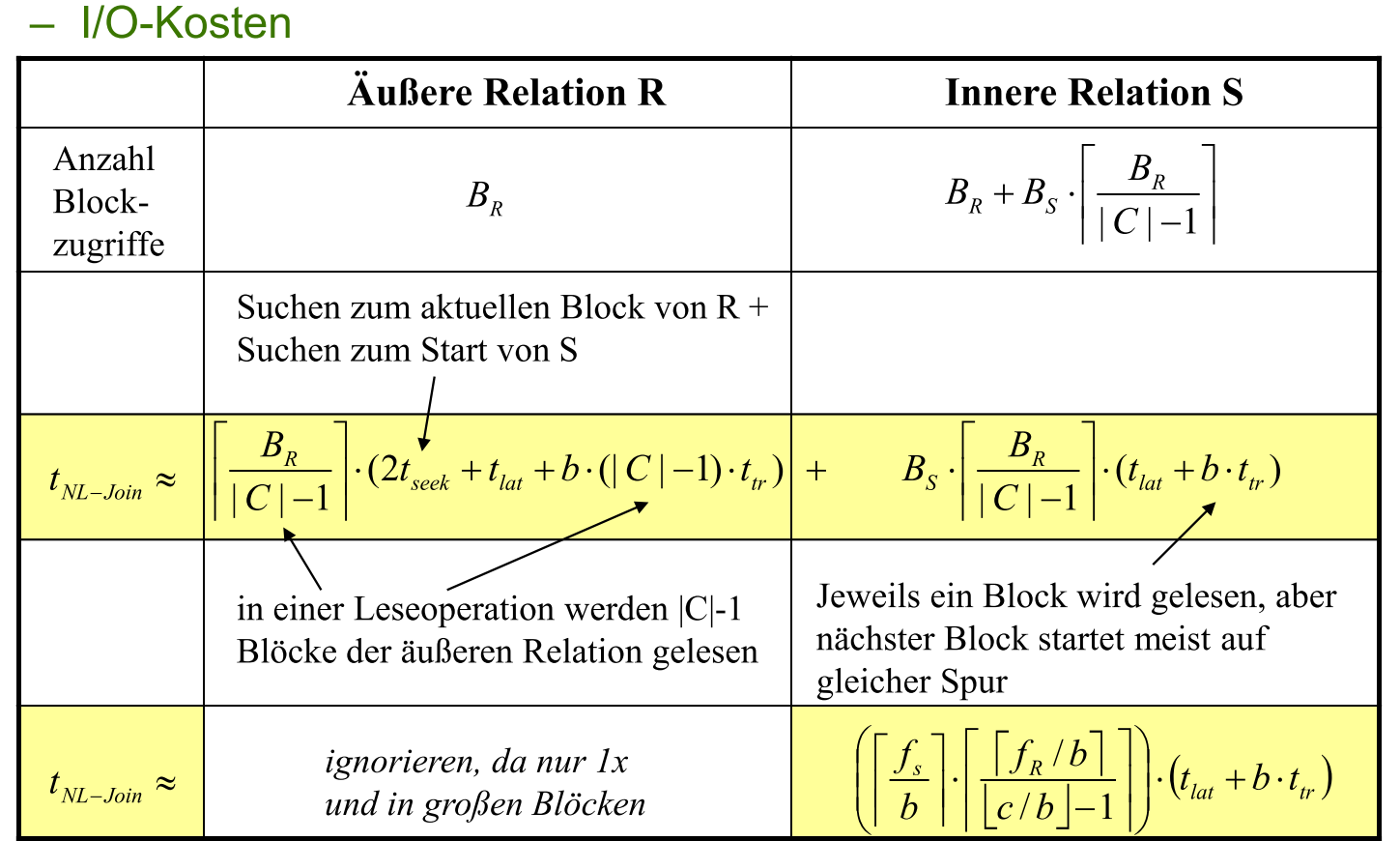

优化函数
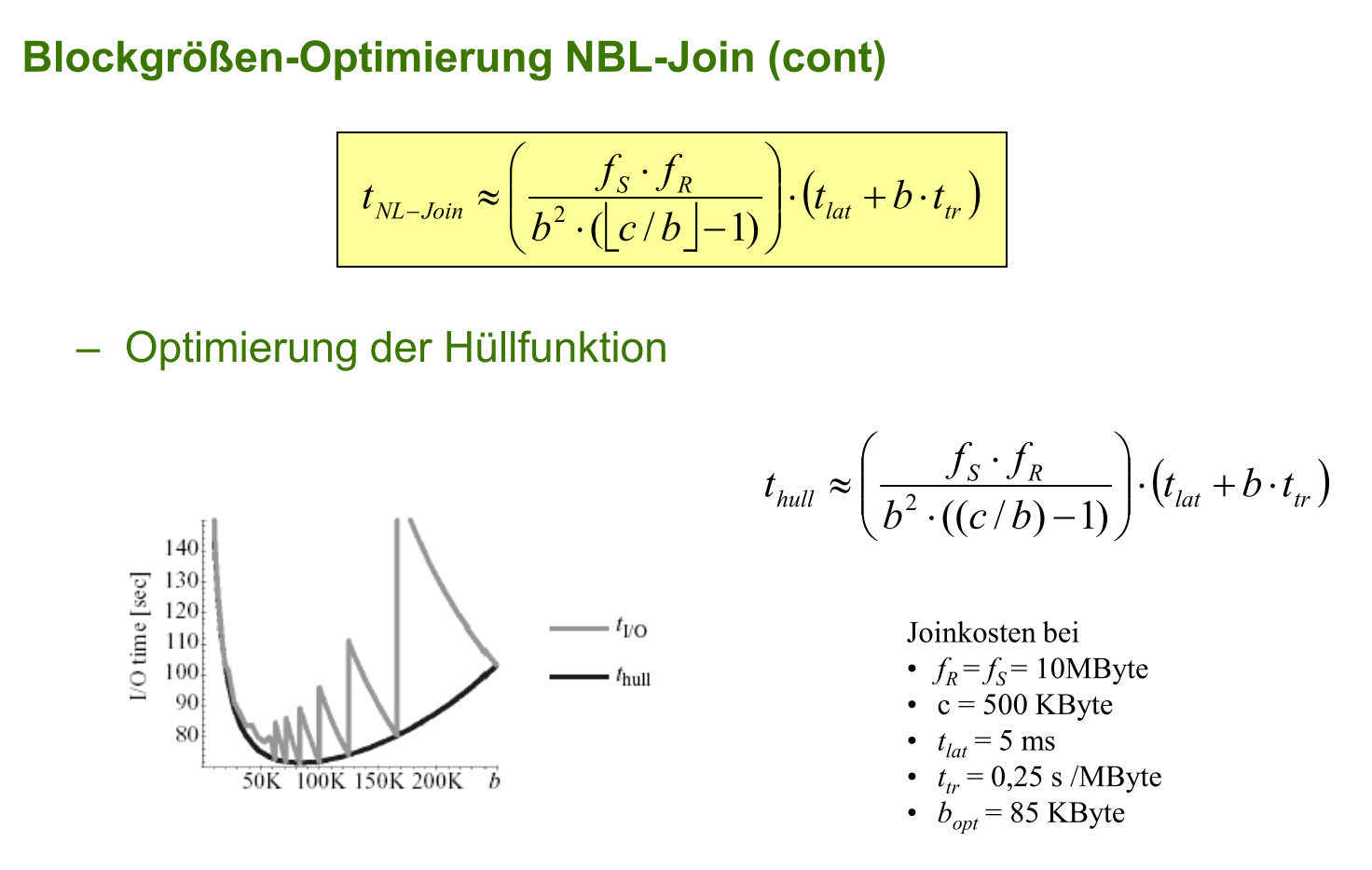 $$0 = \frac{\mathrm{d}}{\mathrm{d}b}t_{hull} \Rightarrow b_{opt} = \frac{\sqrt{t^2_{lat}+t_{tr} \cdot t_{lat} \cdot c}- t_{lat}}{t_{tr}}$$
取正根, 取整后有两个结果
$$b_1 = c/ \left \lfloor \frac{c}{b_{opt}} \right \rfloor,\\ b_2 =c/ \left \lceil \frac{c}{b_{opt}} \right \rceil $$
$$0 = \frac{\mathrm{d}}{\mathrm{d}b}t_{hull} \Rightarrow b_{opt} = \frac{\sqrt{t^2_{lat}+t_{tr} \cdot t_{lat} \cdot c}- t_{lat}}{t_{tr}}$$
取正根, 取整后有两个结果
$$b_1 = c/ \left \lfloor \frac{c}{b_{opt}} \right \rfloor,\\ b_2 =c/ \left \lceil \frac{c}{b_{opt}} \right \rceil $$
实际上, 相比于 CPU 耗时, I/O 耗时是非常低的, 因此需要对 CPU 更友好的算法
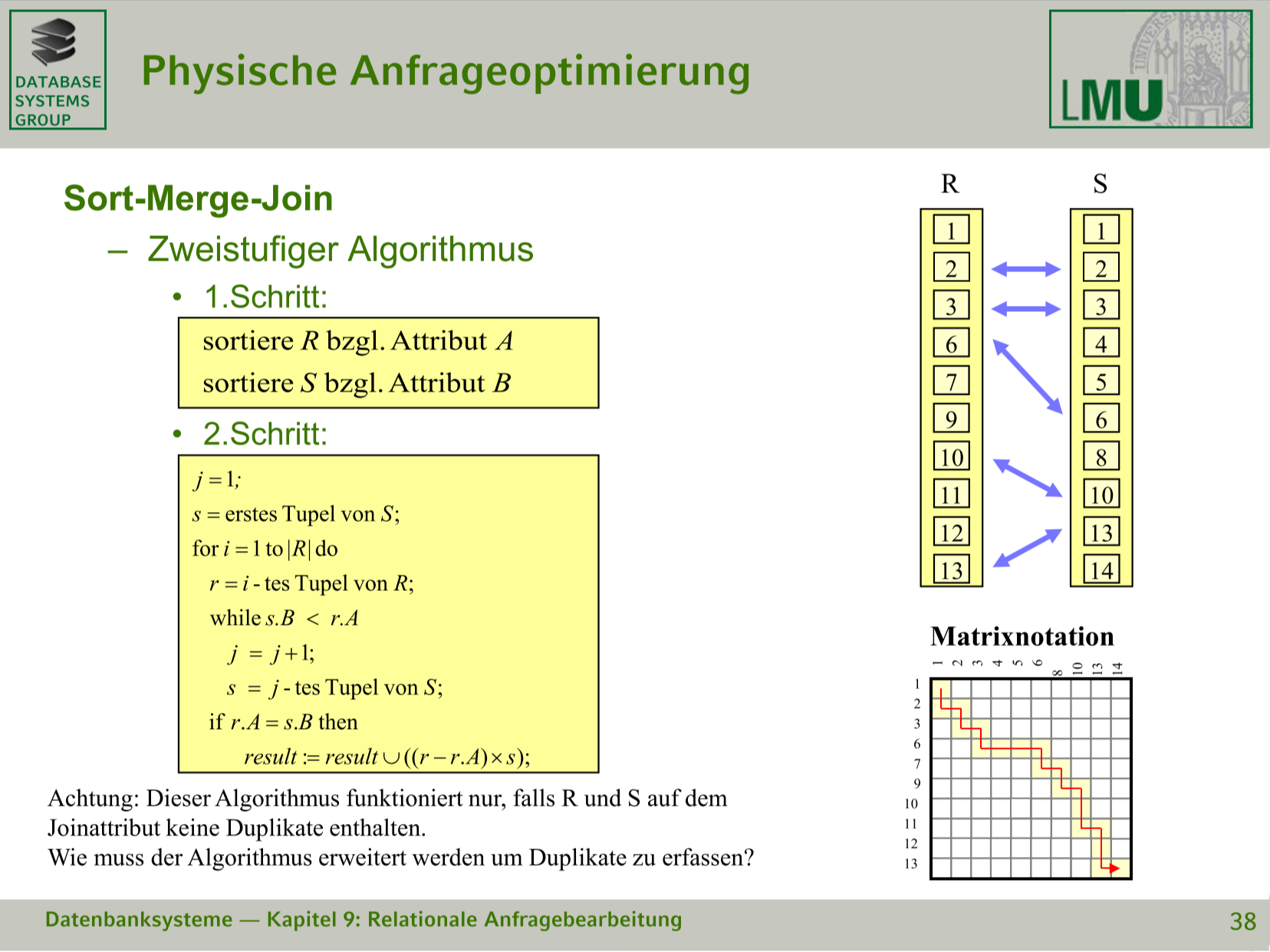
# Sort-Merge-Join
- 把数据排序
- 用双指针法比较
时间复杂度 $O(|R| \cdot \log |R| + |S| \cdot \log |S|)$
# Hash-Loop-Join
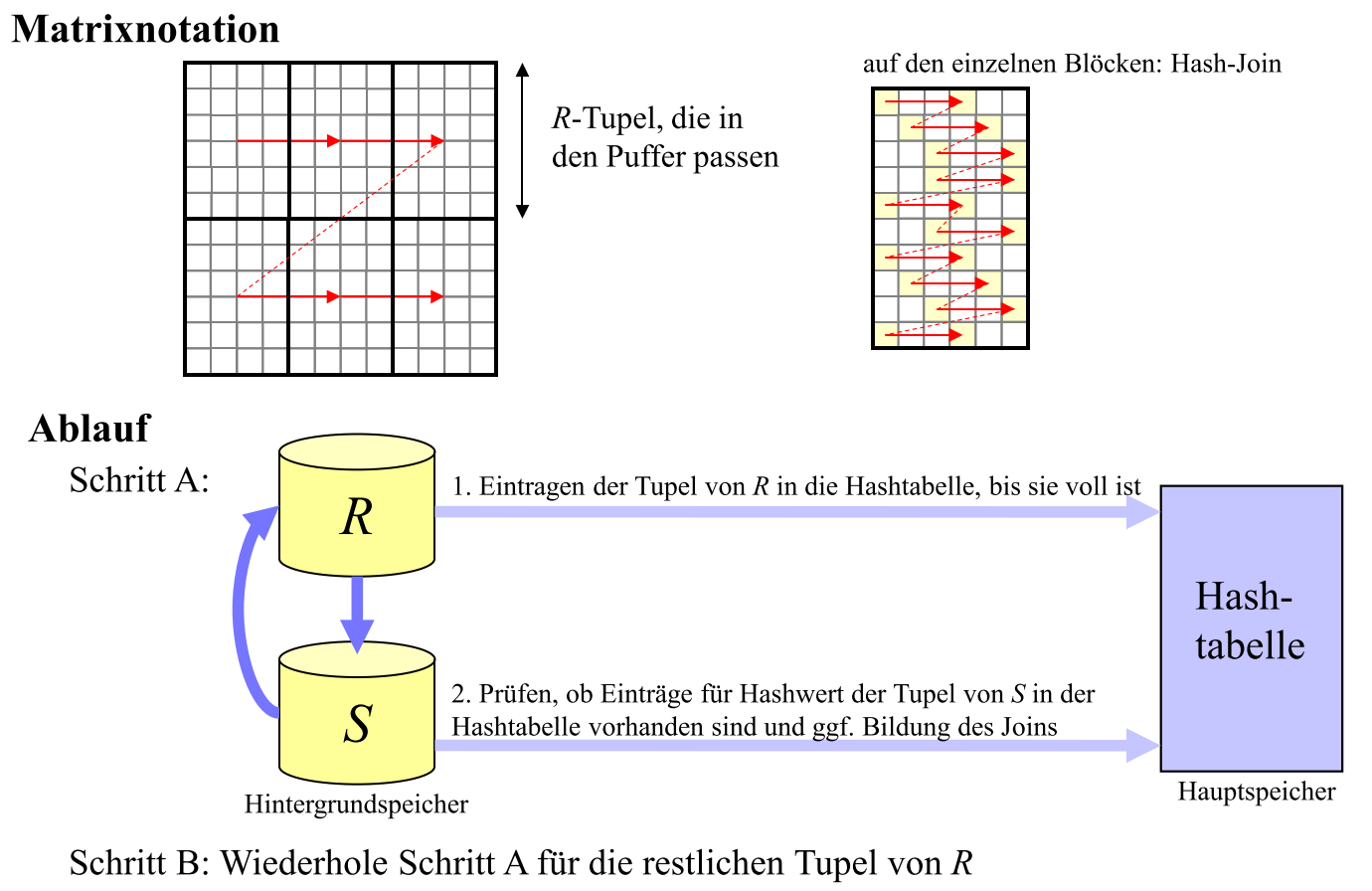
# Naive Hash Join
- 将 R 全哈希了
- 对每一个 s 哈希, 拿哈希表比对
 $O(|R| + |S|)$
$O(|R| + |S|)$
# Hashed Loop Join
每次读取合适数量的 R 哈希, 把所有 S 和这部分比对, 再读取下一部分合适数量的 R, 重复

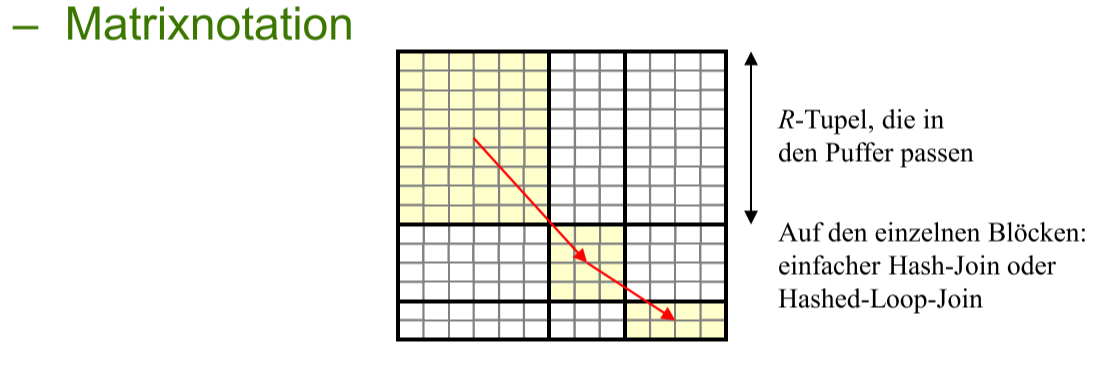
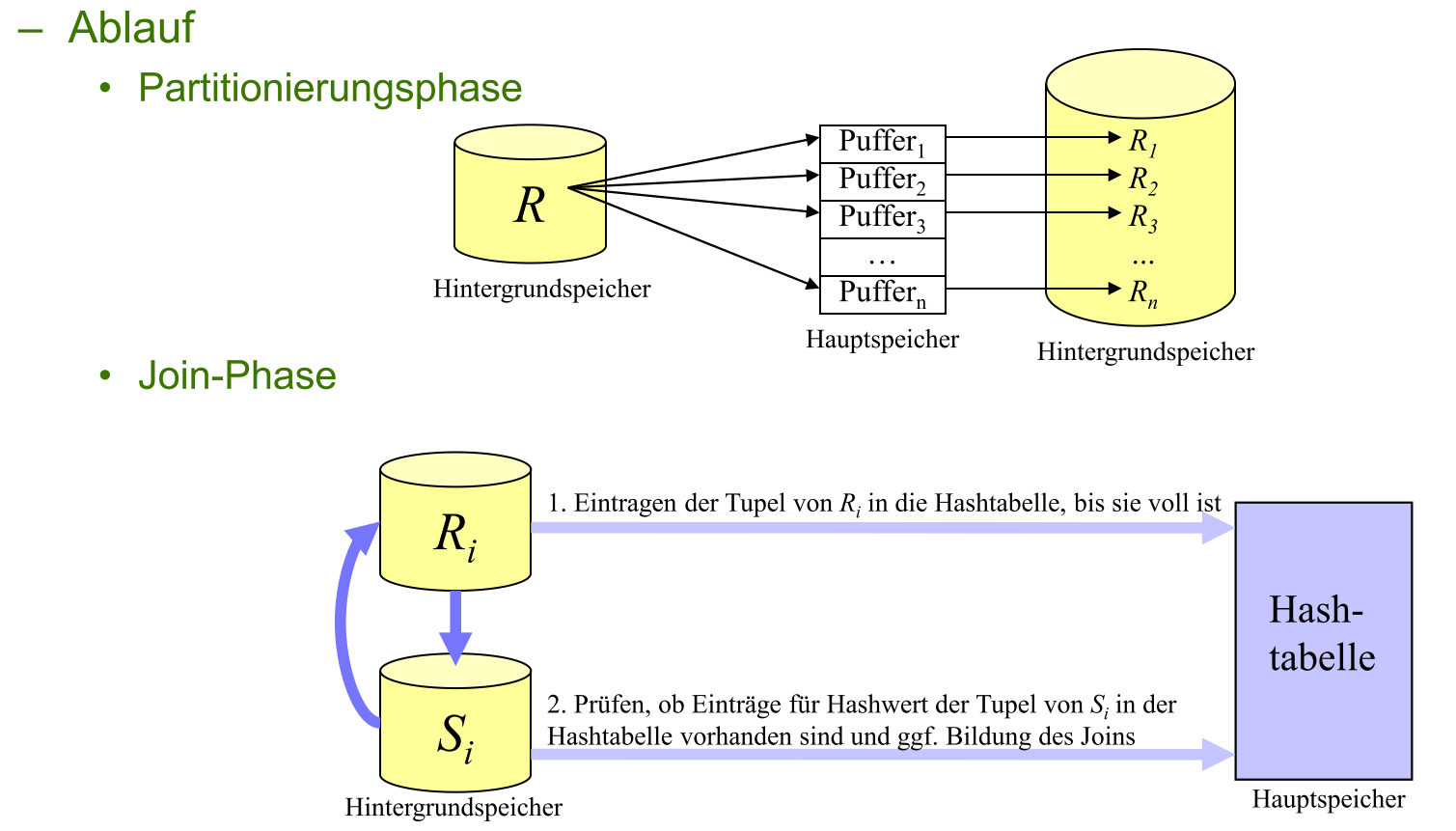
# GRACE / Hash Patitioned Join
不是把每个 r 和每个 s 比对,
而是用 hash function 把 R 和 S 分别划分成 hash key 分区(Partition), 只有具有相同 hash key 的 R分区 和 S分区需要比对
# Transaktionen
# Synchronisation(Concurrency Control)
# Transaktion
transaction
Folge von Befehlen (read, write), die die DB von einen
konsistenten Zustand in einen anderen konsistenten Zustand überführt
对数据库的一系列操作, 其影响是持久性的. 数据库的完整性被保护下的状态变化单元, 主要任务是
- 同步
- 数据恢复
# ACID 原则
# Atomicity
原子性, transaction 的效果要么完整, 要么没有.
# Consistency(maintaining integrity)
consistent 状态 → consistent 状态
# Isolation
一个用户不会觉察其他用户在 transaction 中所做的更改
# Persistence/Permanence
完成的 transaction 的影响永久地保存在数据库
# Transaction 流程控制
# begin of transaction(BOT)
setup 操作, 在 sql 里没有
# end of transaction(EOT)
teardown
sql: commit / commit work
# abort
放弃更改
sql: rollback / rollback work
# 对于 长transaction
- 定义保存点
- 处于活动状态的事务可以回滚到该保存, 不可提交
- sql:
savepoint <identifier>
- 备份 transaction
- 回滚
- sql: `rollback to
# commit 失败
如果检测到 commit 违反约束(如 , 数据的正确性和完整性), 可能会失败.
# 为什么要同步/并发
- 单线太慢, 等待时间长, 吞吐量(leistungsfähigkeit)低
- 可以多用户操作
- 同步可以确保一个用户操作时不受其他用户影响
# Anomalien in Mehrbenutzerbetrieb 多用户操作中的异常
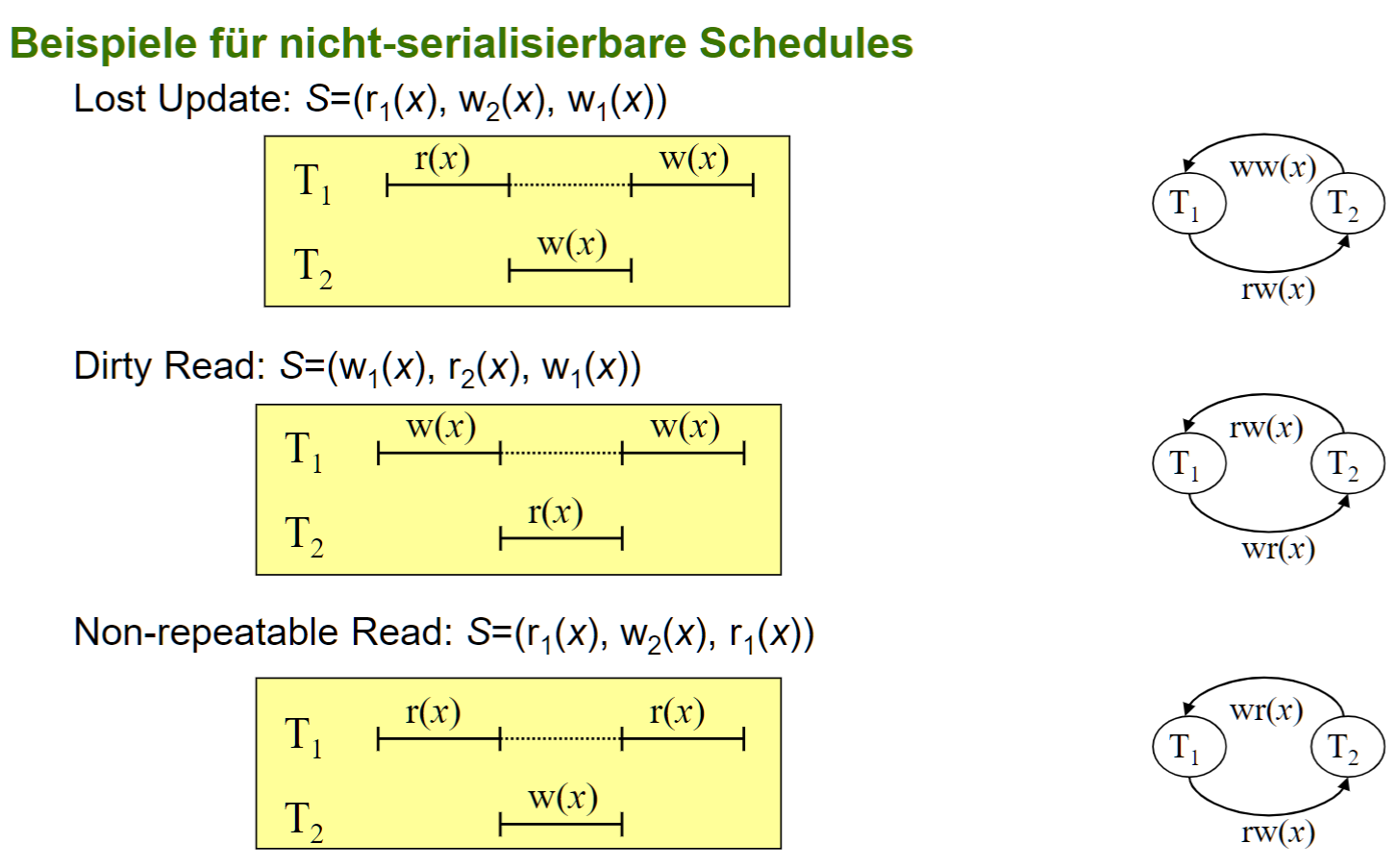
# Lost Updates
违反: Durability
# dirty read/ dirty write
数据状态不是永久有效的,
如果临时状态的数据被读取了, 就叫脏读取
 违反: Durability/Consistency
违反: Durability/Consistency
# Non-Repeatable Read
一个 TA 在执行过程中读取了两次, 值不一样(别的 TA 更改了) 违反: Isolation
# Phantomproblem
不可重现阅读的特例,其中涉及新生成的数据,并且主要在第二个 TA 聚合函数中
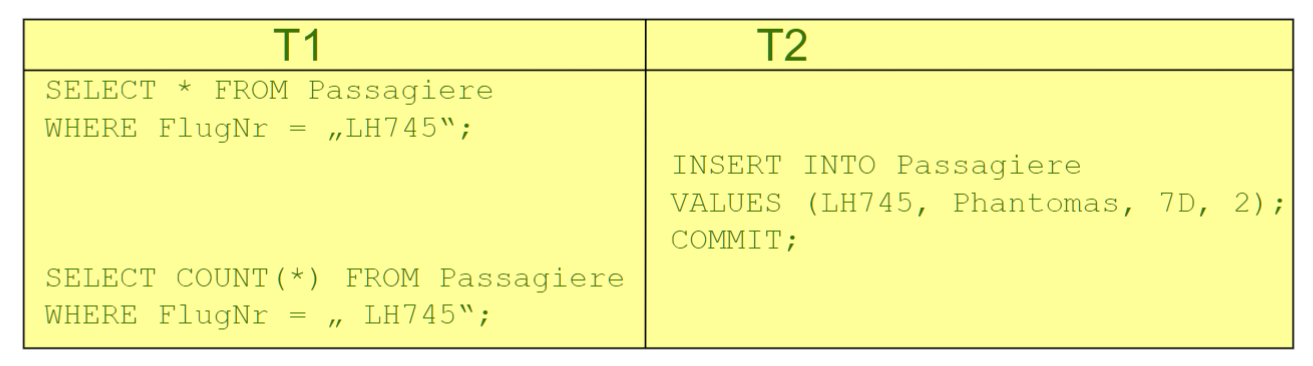 咦, 不是查到 n 项数据吗, 怎么又变成了 n+1 项
咦, 不是查到 n 项数据吗, 怎么又变成了 n+1 项
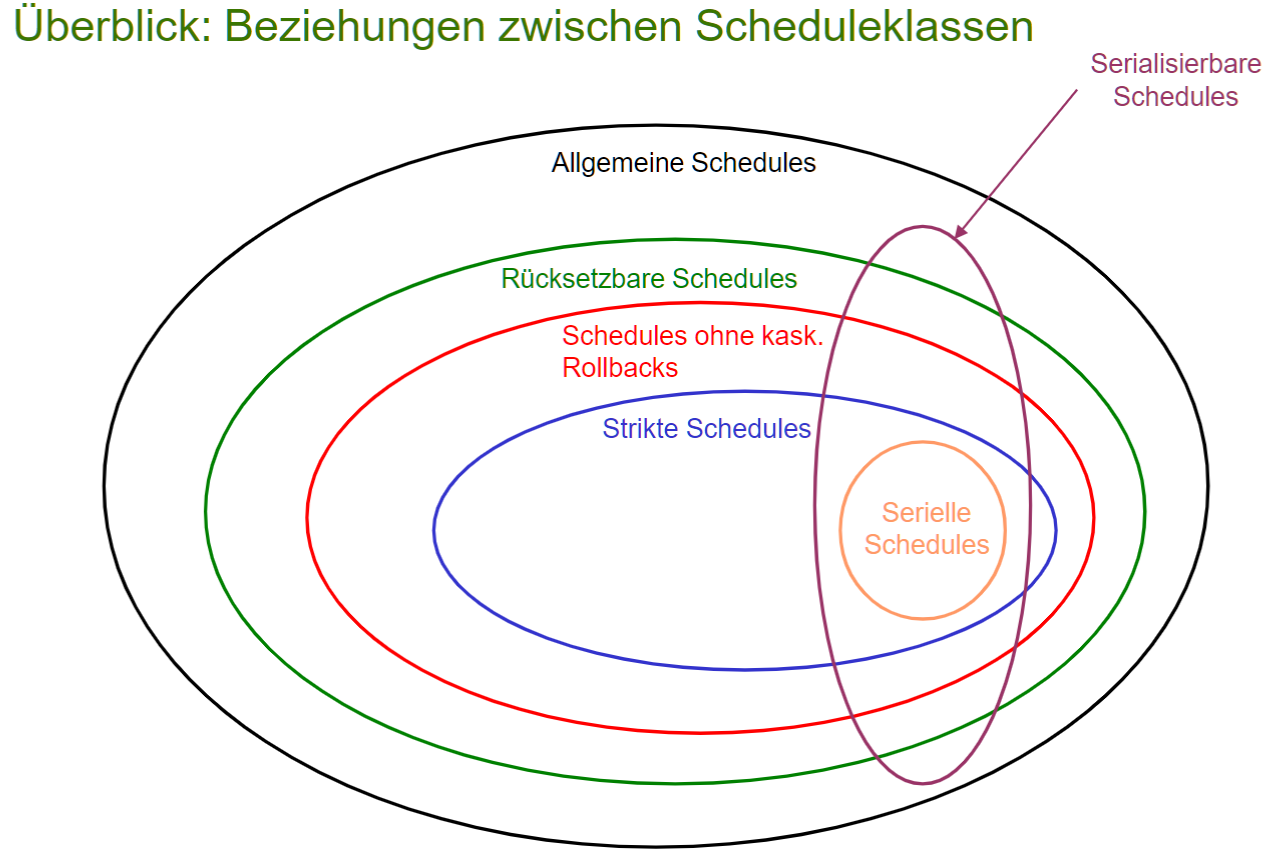
# Serialisierbarkeit von TA
指一个一般调度是否能转化为一个串行调度 Motivation
- 对用户隐藏并发
- 对用户透明, 即感觉 TA 在以任意顺序连续执行, 而不是和其他 TA 交错
# Allgemeiner Schedules 一般调度
Schedule(history) 是集合 {$T_1$, …, $T_n$}, 是 TA 的行动序列. 它对交易 $T_i$ 的顺序(存在穿插)洗牌, 但会保留每个 TA 的内部顺序
一般调度显然提供了任意的联锁,因此出于性能方面的考虑,需要一般调度。
# Serieller Schedule 串行调度
各 TA 的操作没有交错, 而是一块一块执行. 从 Isolation 的原则看, 需要串行调度
# Serialisierbarer Schedule 可序列化调度
Ein (allgemeiner) Schedule S von {T1 , …, Tn} ist serialisierbar, wenn er dieselbe Wirkung hat wie ein beliebiger serieller Schedule von {T1 , …, Tn} . 可序列化调度是存在等价串行调度的一般调度. 是一般调度和串行调度的折衷. 得到的等价调度称为 Serialisierungsreihenfolge
# Abhängigkeit
# Schreib-Lese-Abhängigkeit $T_i$ → $T_j$
对某一项 x, w$_i$(x) 应该在 r$j$(x) 前 Abkürzung: wr${i,j}$(x)
# Lese-Schreib-Abhängigkeit $T_i$ → $T_j$
对某一项 x, r$_i$(x) 应该在 w$j$(x) 前 Abkürzung: rw${i,j}$(x)
# Schreib-Schreib-Abhängigkeit $T_i$ → $T_j$
对某一项 x, w$_i$(x) 应该在 w$j$(x) 前 Abkürzung: ww${i,j}$(x)
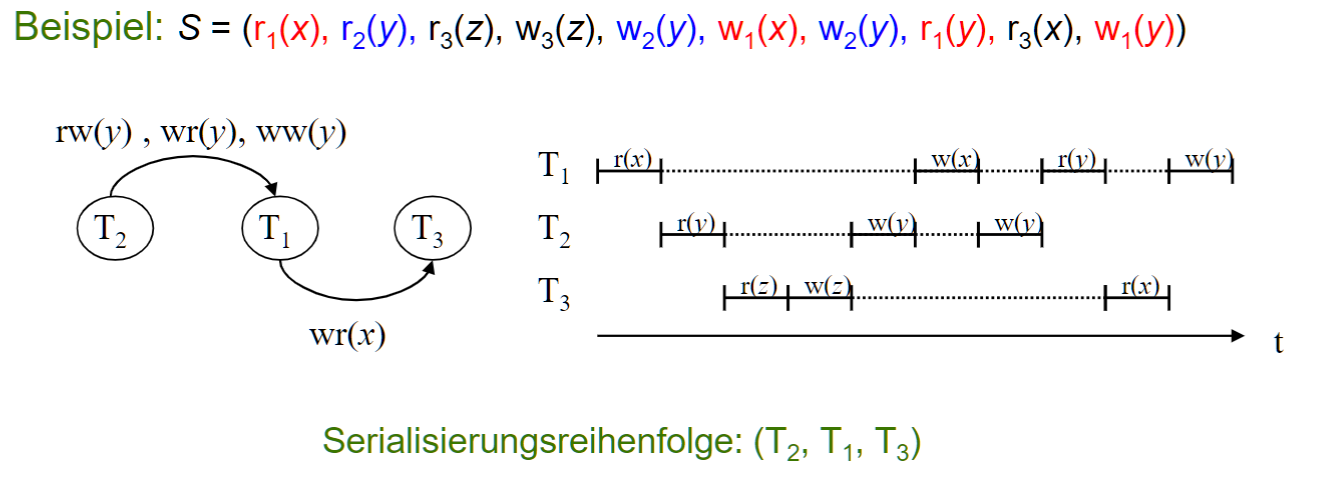
# Konflikt-Äquivalenz 冲突等价
如果说 调度 S1 和 S2 等价, 那他们的 TA 以及 TA的依赖() 就应该是等价的. 即比如说, 如果 S1 中读某个项的值是 x, 那 S2 读到的也应该是 x.

# Serialisierungs-Graph
- 用于检查两个调度是否冲突等价
- TA 是 Node
- 依赖是 Edge
- Ein Schedule ist serialisierbar, falls der Serialisierungs-Graph zyklenfrei ist
- 通过对图的拓扑排序, 可以得到 Serialisierungsreihenfolge (如果有的话)
- 通过图的方法计算可序列化性的成本太高, 因此通常用其他方法, 如被动管理()或在结束后主动检查
# Rücksetzbarer Schedule 可撤销调度
T$_i$ 只有在其读取了数据的 T$_j$ 结束后, 才能执行 commit
# Schedule without cascading reset
没有级联 reset 的调度 进行中的 TA 涉及的数据禁止读取
# Strikter S.
# Locking
# Lock(Sperre)
- LOCK()/UNLOCK() atomar(不可打断)
- Sperrgranularität: Datenbank, DB-Segment, Relation, Index, Seite, Tupel, Spalte, Attributwert
- Sperrenverwalter 执行锁
# Legal Schedule 合法调度
- 每次访问一个对象前都会设置适当的锁, 最迟在 TA 结束时解锁
- 等待已有的锁
- lock/unlock 应在 DBMS 中隐式完成
- 合法调度并不一定是可序列化调度
# Zwei-Phasen-Sperrprotokoll(2PL)
- 最简单和最常用的
- 在上锁结束前不解锁
- 两个阶段:
- Wachstumsphase: Anforderungen der Sperre
- Schrumpfungsphase: Freigabe der Sperre
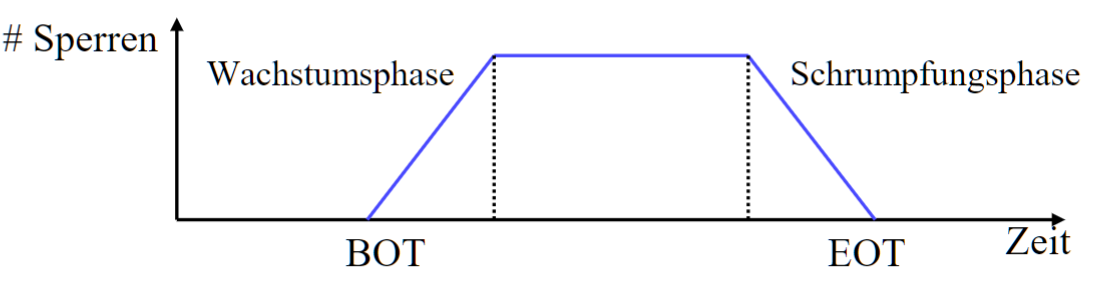
- 问题: 不能撤回
# Striktes Zwei-Phasen-Sperrprotokoll(Striktes 2PL)
- 在 2PL 的基础上, 所有锁保持到 COMMIT
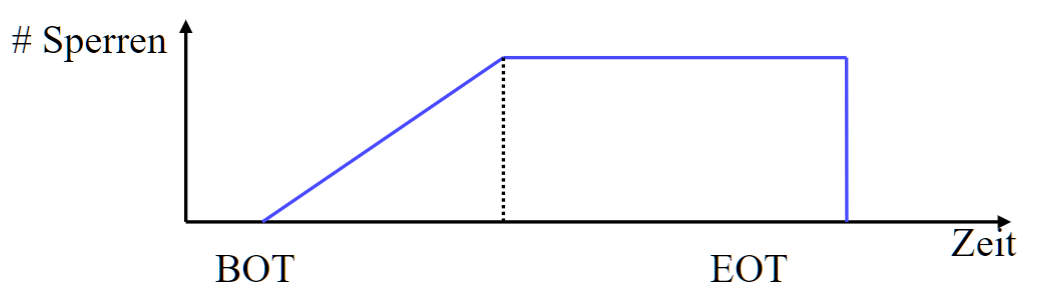
- 保证可序列化, 可搜索的调度, 但 TA 的 并行度(Paralleilisierungsgrad) 受到严格限制
- 问题: 过于严格了, 实际上纯读取是可以并行的(无级联)
# RX-Sperrverfahren
- 允许纯读取 TA 之间并行
- 主要与Striktes 2PL结合使用, 仅能得到无级联的可撤销调度. 得到的 Serialisieungsreihenfolge 由第一个冲突操作决定
- 可能造成死锁(Deadlock, Verklemmung)
# Datensicherheit(Recovery)
# Fehler 和 Recovery 的分类
# Transactions Recovery
Transaktionsfehler(未确认的 TA 的错误)
- 程序错误
- ROLLBACK
- Sync Conflict
- Verletzung von Regeln
通过 Rücksetzen 解决
- local UNDO(如撤回某个 TA 的操作)
- 这类错误很常见, 所以解决方法应在 mm 级完成
# Crash Recovery
System Error(死机那类)
通过 Crash Recovery(Warmstart) 解决
- global UNDO: 重置所有已进入 DB 但未完成的 TA
- global REDO: 更新所有已完成但未进入 DB 的TA
- 通常频率可能在几天一次, 恢复需要数分钟
# Geräte Recovery
Medien Error
- Plattencrash
- Wasserschaden
- 系统程序导致的数据丢失
通过 Geräte-Recovery(Coldstart) 解决
- 恢复到较早的, 安全的数据库状态
- global REDO: 更新所有在备份副本创建后完成的 TA
- 介质错误很少发生, 通常是几年一次. 且需要提前备份
# Logging
任务: 所有操作(DO)都需要日志条目, 以得到 UNDO 或 REDO 时需要的信息
- physisch
- Zustandslogging
- Seitenlogging
- Eintragslogging
- Übergangslogging
- Zustandslogging
- logisch
- Übergangslogging
- physiologisch
# Physisches Logging
在物理对象(Seiten, Datensätze, Indexeinträge)层面记录
Zustandslogging: 记录更改前后的值
- Seitenlogging: 页面级别的记录, 恢复快速, 但页面锁定->高冲突率. 记录页面的完整副本所以占空间&高I/O成本
- Eintragslogging: 只有实际改变的条目被记录, 锁定粒度更小. 收集在缓冲区内->显著减少磁盘访问. 恢复更复杂, 需要将更改的Seite完全加载在主内存中才能使用(通过异或)
Übergangslogging: BFIM(before image) 和 AFIM(after image) 的差异
# Logisches Logging
使用当前参数记录更改, 在更高的抽象级别
REDO 的问题:
- 更改通常包括多个 Seiten, 原子(操作)的 Einbringen 困难
- 比物理更昂贵
UNDO 的问题:
- 面向数量的更改可能导致非常昂贵的日志条目
- Bsp.:
DELETE FROM Products WHERE Group = ‘G1’=> UNDO erfordert viele Einfügungen, falls Produktgruppe G1 umfangreich ist - Bsp.:
UPDATE Products SET Group = ‘G2’ WHERE Group = ‘G1’=> UNDO muss alte und neue Produkte der Gruppe G2 unterscheiden
- Bsp.:
# Physiologisches Logging
- Physical-to-a-page: 记录单位是更改的page, 与缓冲区管理和直接原子Einbringen 很兼容
- Logical-with-a-page: 一个页面上的变化用逻辑记录
好处
- Log条目 不会像逻辑日志那样引用多个页面
- Log Data(数据量): logical < physiological < physical
# Log data
记录类型
- Begin, Commit, rollback of TA
- DB状态 经过 TA 后的变化
- checkpoints
Components of Änderungseinträgen
- LSN(Log Seq. Number): 按时间排序的唯一表示符
- TA-Id: (进行更改的) TA 的唯一标识符
- Page-Id
- REDO: 指示如何跟踪更改
- UNDO: 指示如何逆转更改
- PrevLSN: 指向各 TA 的前一个日志条目的指针(没有上一个则为0)
Log data 的数据结构
- Ringpuffer, sequentielle
- 只需要一定时间内的记录
- Crash Recovery: UNDO 记录 在 TA 完成后就不再需要了
- Geräte Recovery: 需要 Archive Log

# Abhängigkeiten zu anderen Systemkomponenten
# Speicherhierarchie
DBMS-Puffer/DB-Puffer 进行中的 TA 都在这里执行
DB ACID consistent 才放进去, COMMIT 就是到这里
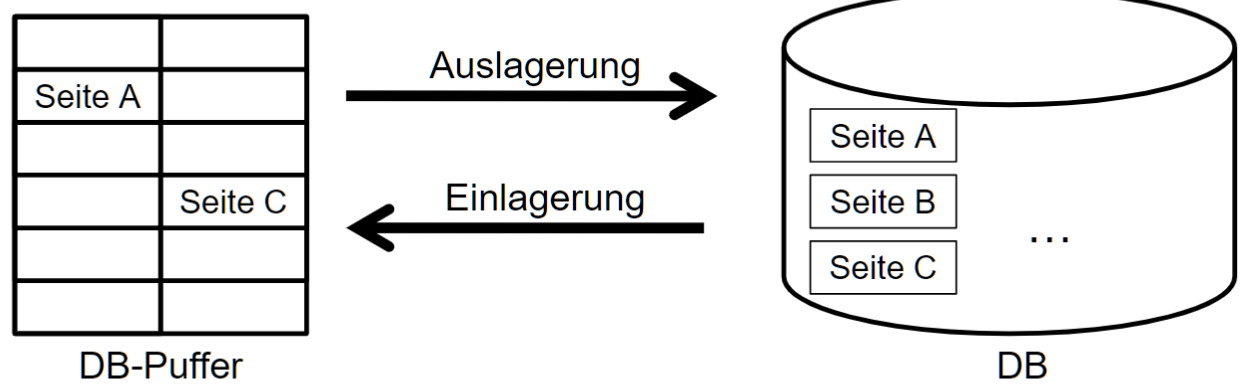
# 依赖总览: 在DB的操作中需要管理什么
Pufferverwaltung
- Verdrängungsstrategien: Puffer voll?
- Ausschreibestrategien: wann schreibe ich Änderungen aus?
HGS-Verwaltung
- Einbringungsstrategien: wie schreibe ich Änderungen aus?
综上, wann schreibe ich Log-Datei auf Platte? Recovery/Logging 也依赖锁管理

# Einbringungstrategie
# Direktes Einbringen
- Non-atomic(不能随时打断), Update-in-Place
- 当今 DBMS 最常见的方法
- 每个 Seite 在 Platte 上有一个专门的地址, 更改 Seite 就是在 DB 覆盖原本的内容
- UNDO 信息必须显示存储

# Indirektes Einbringen
- Atomic
- Seite 在 Platte 有两个副本
- Twin-Block-Verfahren: 每个 Seite 都有两个 Block
- Scattenspeichertechnik: 只有改变过的 Seite 有两个 Block
- 通过 Seitentabelle umschalte 记录更改的页面, 改完切换状态, 可以保证 atomic
- 修改前的信息也保留了, 因此不用显式记载 UNDO 信息
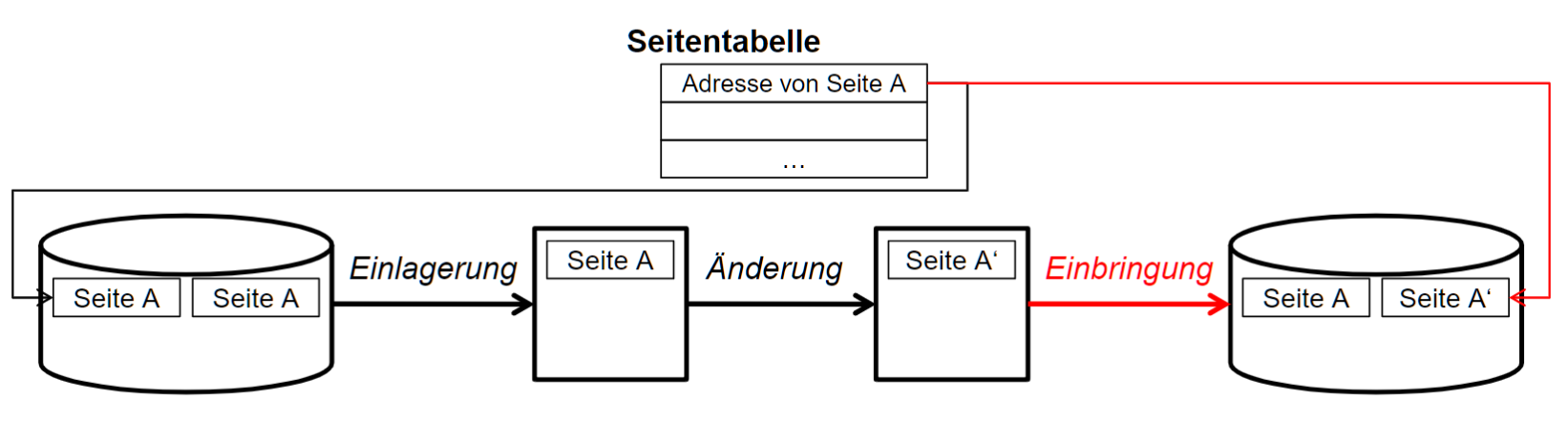
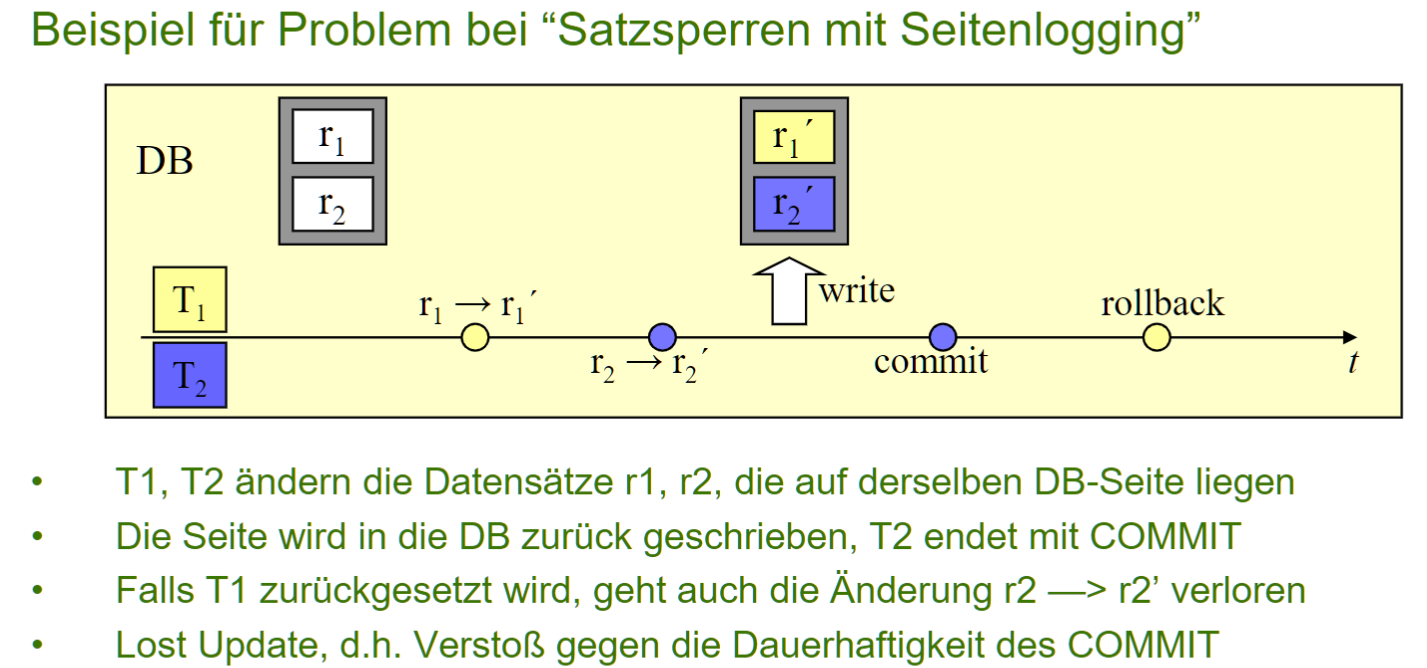
# Einfluss der Sperrgranularität
- Log granularity <= Lock granularity, 否则可能 Lost Update
- 下面这个例子, log(seite)>锁(条目), 就出问题了
# Verdrängungsstrategien
置换策略: 什么时候替换缓存区的脏页
Schmitziger Seiten SeitePuffer $\neq$ SeiteDB
如果是脏页:
# No-Steal
- 不得从 Puffer 移除脏页, DB 不包含不成功的 TA
- 不需要 UNDO Recovery
- 更改仅可能在 COMMIT 后到达 DB(与Force冲突)
- 长更改 TA => 大部分 Puffer blokiert => 限制并行
# Steal
# Ausschreibestrategien
EOT操作, 什么时候把更改带进 DB
# Force
- 所有更改最迟在 EOT(COMMIT 前) 写入 DB(与No-Steal冲突)
- 每个更改是逐个写入的 => 高IO, 响应慢, 锁定时间长
- 在系统错误时不需要 REDO
- 大型 DB-Puffer 使用不当
# No-Force
# Puffer Verwaltung

# Steal/No-Force
- 需要 REDO, UNDO, 但是是最通用的解决方案
- 实际效果最好
# No-Steal/Force
- 因为冲突, No-Steal => No-Force, Force => Steal
- 牺牲 COMMIT 的效率, 优化错误情况
# WAL-Prinzip und COMMIT-Regel
# WAL-Prinzip (Write-Ahead-Log)
- UNDO Info (e.g. BFIM) 必须在 DB 更改前记录
- Steal/direktem Einbringen
# COMMIT-Regel(Force-Log-at-Commit)
- REDO Info (e.g. AFIM) 必须在 DB 更改前记录
- Crash-Recovery&No-Force 必须
- for Geräte Recovery Force/No-Force 必须
# Commit Verarbeitung
# Standard Zwei-Phasen-Commit
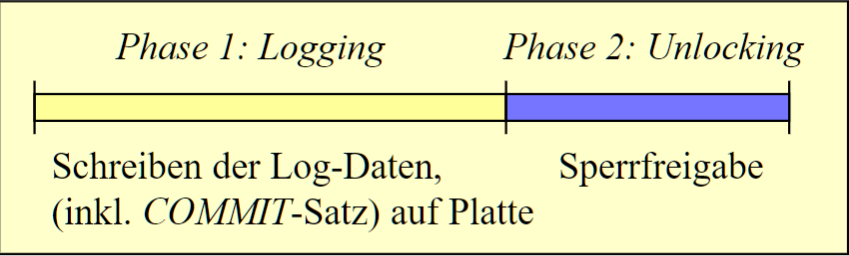
Phase 1: Logging
问题
- COMMIT-Regel 要求每次 COMMIT 写出(Ausschreiben) Log-Puffer
- 对短 TA 性能退化
- TA 的 Durchsatz 受限
# Gruppen-Commit
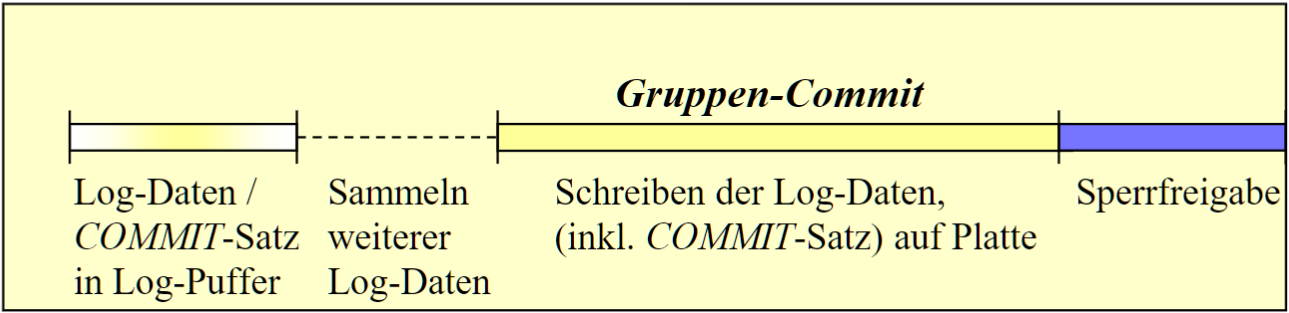
- Log data 在 Log Puffer 收集多个 TA
- Log Puffer 满了的时候, 或者到一定时间, 将 Log Puffer 里的内容写到磁盘
- 优点: 减少磁盘读写
- 缺点: 锁时间长, 回应时间长
- 现实中很多 DBS 支持
# Pre-Commit
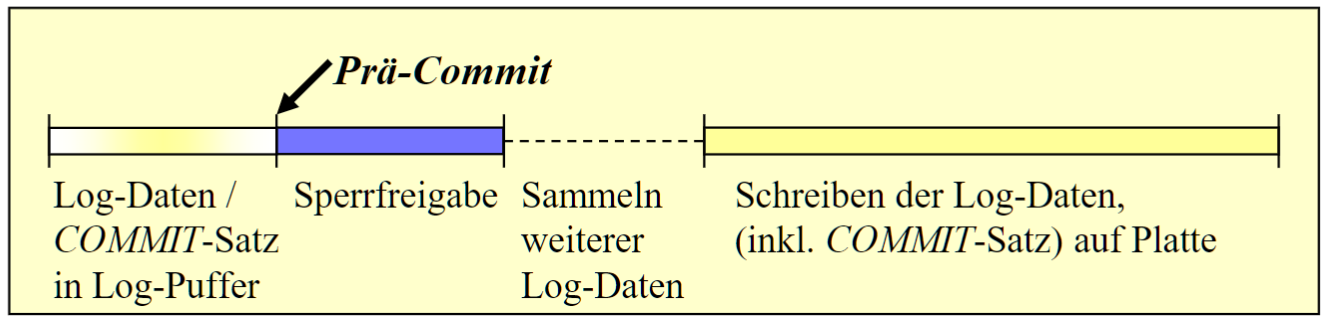
- 为了避免 中的长时间的锁, 在 COMMIT 信息写入 Log Puffer 时就会 unlock
- 关于产生的脏读取(也不完全是脏, 毕竟在 log 中 commit 了)
- 正常情况:改变的 TA 成功结束,改变是有效的
- 错误情况:只有在系统错误的情况下才可能终止 TA ;在系统错误的情况下,其他运行的 TA 也被终止,“脏读取"因此不能影响DB
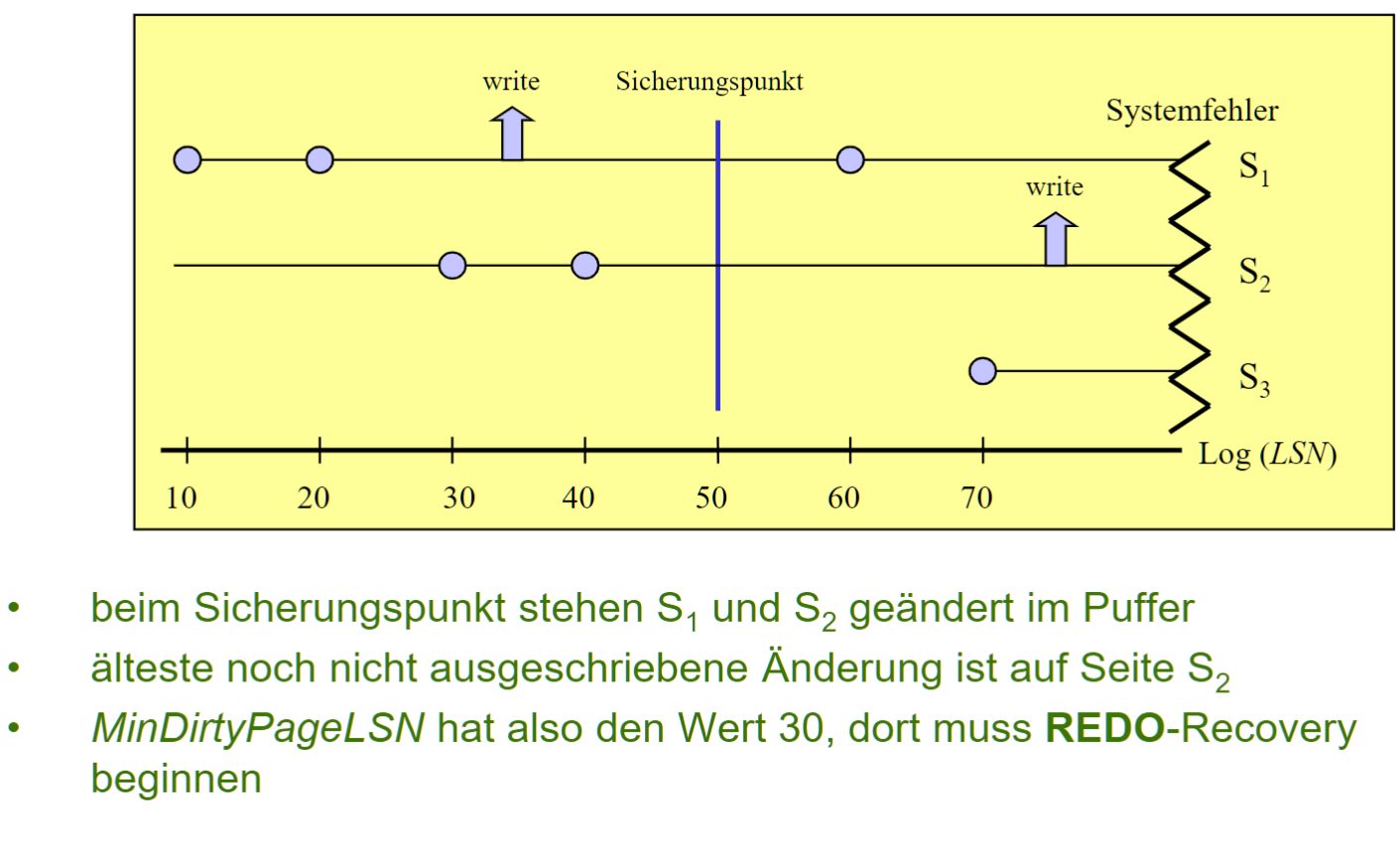
# Sicherungspunkt
- 检查点是用来表明 REDO 界限的措施, 太少=>高 REDO 成本; 太多=>高正常流程成本
- 如果没有检查点, 自 DBMS 开始以来的所有更改都可能重复. 对 Hot Spot Seiten 尤其重要(几乎不会从缓冲区移出的热点页面)
# Checkpoint 的实现
特殊的日志条目:
|
|
最后一个完全执行的保存点的 LSN 会保存在 restart data 中
# Direkte Sicherungspunkte
- 所有改变了的 页面 都在检查点写入 persistente DB(Platte)
- 备份需要的时间和备份时间间隔成正比
- Multi Page Access 有助于减少磁盘写入头的定位数
- REDO 可以从最后一个完全执行的检查点开始
# TOC
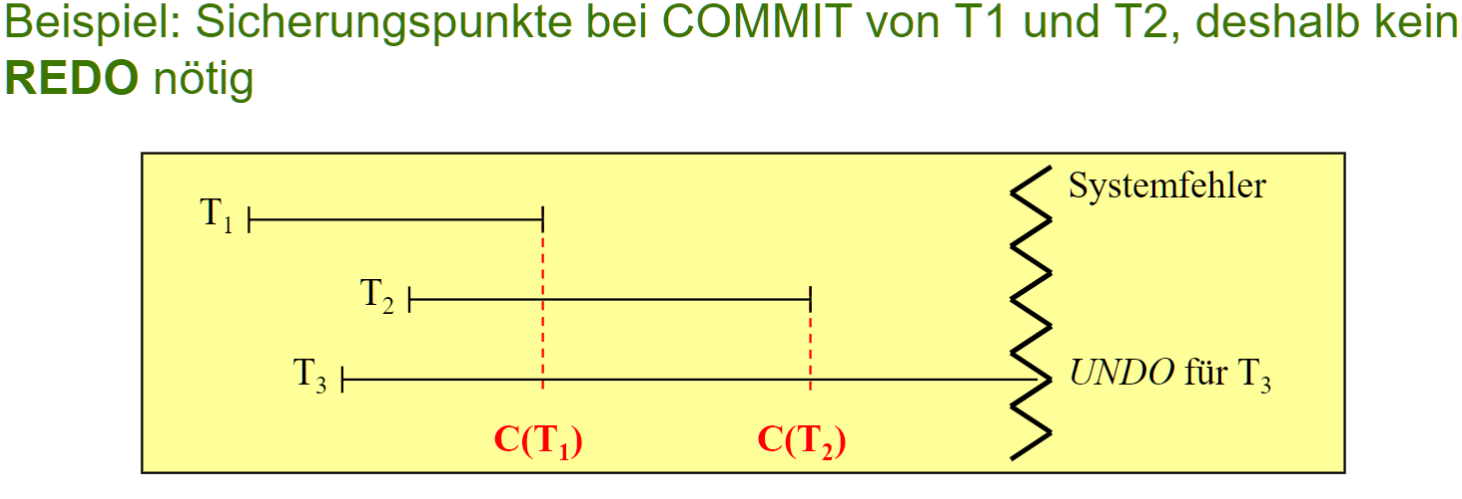
Transactions Oriented Checkpoint
- 在每个 TA 提交时强制设置检查点
- 只将缓存中与该 TA 相关的 页面写入磁盘, 而不是缓存中的所有
- 需要 UNDO, 不需要 REDO (Force => Steal)
- 优点
- 不需要 REDO, 从最后一个检查点 UNDO 恢复(然后重新开始未确认的 TA)
- 与 页面锁 结合, 实现起来很容易
- 缺点
- 正常流程成本高, 尤其是 Hot Spot Seiten
# TCC
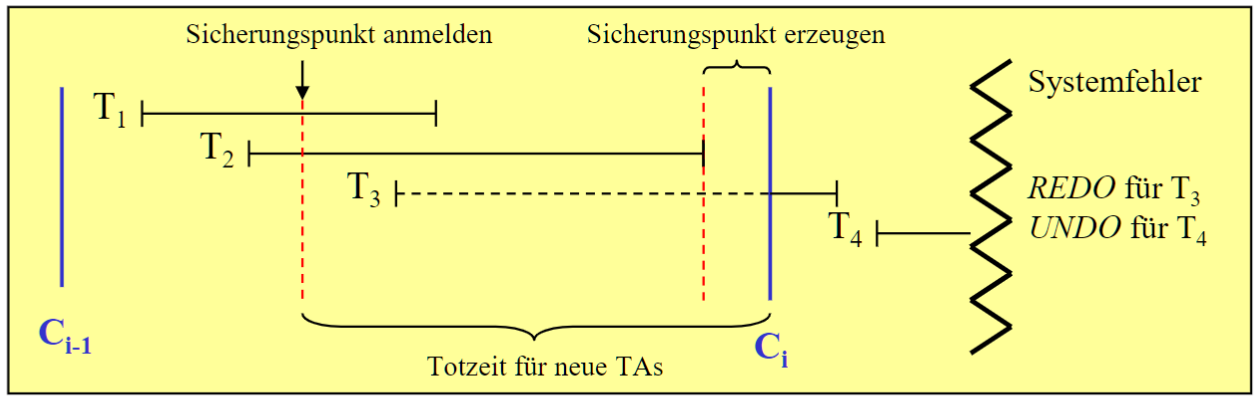
Transactions Consistent Checkpoint
- 在 没有脏变化/没有进行中的TA/consistent 时, 创建检查点
- 通过最后一个检查点 REDO 和 UNDO
- 操作: 注册检查点 -> 等进行中的 TA 完成 -> 创建检查点(新来的TA等待创建完成)
- 优点
- 从最后一个检查点 REDO&UNDO 恢复
- 只有最后一个检查点之后的 TA 受到影响
- 缺点
- 系统等待时间长(“死机"时间)
- 系统等待时间长(“死机"时间)
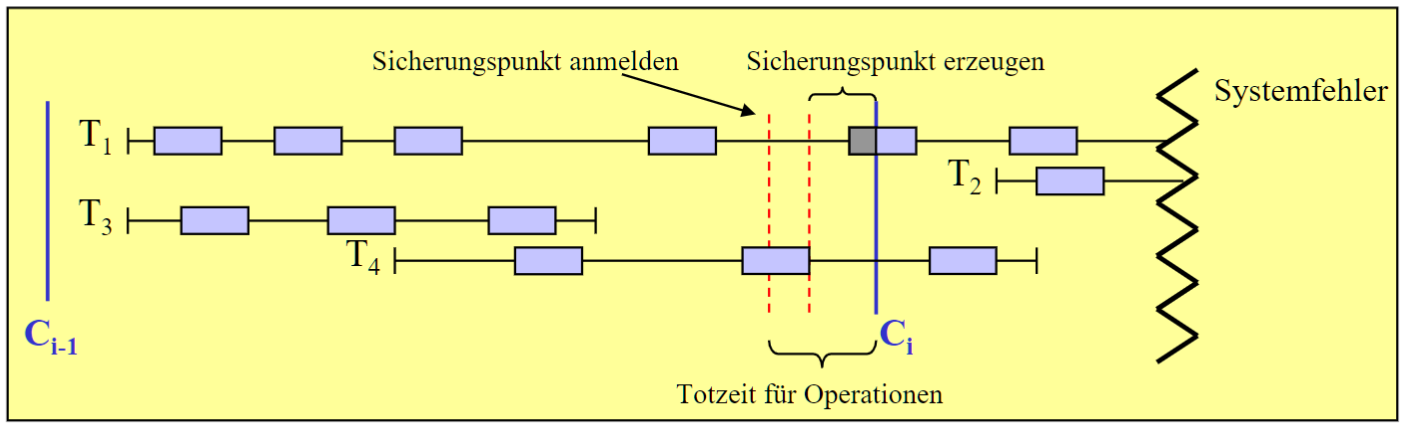
# ACC
Actions Consistent Checkpoint
- 与 相比, 不是确保 TA 完成, 而是确保没有更改操作
- 操作: 注册检查点 -> 等进行中的 更改操作 完成 -> 创建检查点(新来的更改操作延后到检查点创建完成)
- UNDO 恢复: 从 MinLSN(最后一个检查点中, 仍在活动中的 TAs 中的最小 LSN)
- REDO 恢复: 从最后一个检查点开始
- 优点
- 缺点
- UNDO 不能从最后一个检查点开始
- 检查点质量差: 脏更改可能进入 DB
# Indirekte Sicherungspunkte
- 更改不是完全的写入(direkte: 其高成本对大型 DB-Puffer 是不可接受的)
- DB 没有 Actions/TA-consistent 状态, 而是 fuzzy 状态
创建 indirect checkpoint
- 基本上是记录 进行中的TA的状态 和 改变的Seiten
- 最小的写入成本, 几乎对运行没有影响
DB 更改的写出
-
除了 Checkpoint, 进行中的 TA 异步处理
-
对很久没变的页面, 预测性地写出
-
对 热点页面:
- 日志到达指定大小(Log-Umfang)时强制写出
- 建立一个副本, 以免影响新的更改
-
UNDO 恢复: 从 MinLSN(最后一个检查点中, 仍在活动中的 TAs 中的最小 LSN)
-
REDO 恢复: 从 MinDirtyPageLSN = min(StartLSN)
- 对所有更改过页面, 记录 StartLSN
- StartLSN: 自上次从磁盘读取以来, 第一个更改操作的 LSN
# Allgemeine Prozedur der Crash-Recovery
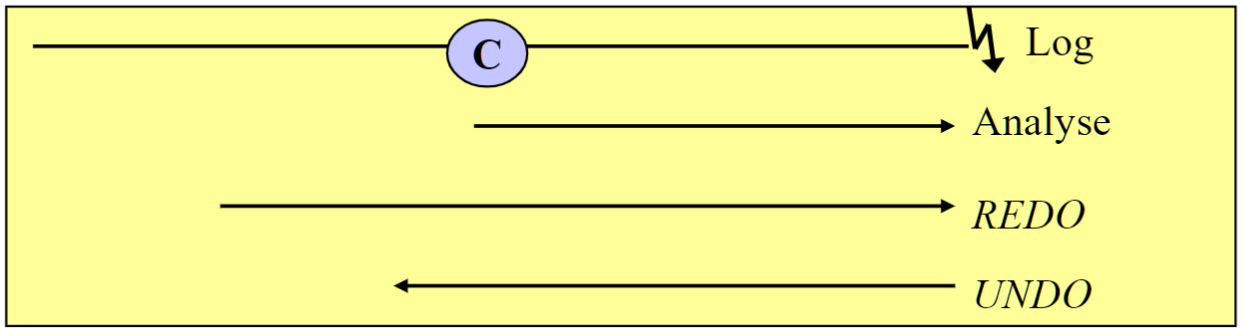
- Analyse-Phase
- 读取上一个检查点以来的所有 Log data
- 确定 Gewinner TA 和 Verlierer TA
- Gewinner TA: Log 中有 Commit 的 TA
- Verlierer TA: Log 中没有Commit 或 有ROLLBACK 的 TA
- 调查检查点后更改过的所有其他页面
- REDO-Phase
- 向后读取 Log (起始点取决于备份类型)
- 重复没有写入 DB 的更改
- 方法1 redo all: 重复所有更改
- 方法2 selective redo: 只重复 Gewinner TA 的更改
- UNDO-Phase
- 向前读取 Log, 直到最旧的 Verlierer TA 的 BOT
- 撤销所有 Verlierer TAs, 直到达上一个检查点时最旧的活动的 TA
- 方法1 redo all(嗯redo): 只撤销到 错误节点 时仍在活动的 TA
- 方法2 selective redo: 撤销所有 Verlierer TA
- Abschluß der Recovery durch einen Sicherungspunkt
# Recovery of Recovery
- 如果在恢复期间发生错误, 就会重新开始 Recovery of Recovery, 所有阶段都要重新开始.
- REDO 和 UNDO 阶段必须是 idempotent 的, 即使多次执行, 总是提供相同的结果. 即对每个 更改操作 A, 有:
- UNDO(UNDO(…UNDO(A)…) = UNDO(A)
- REDO(REDO(…REDO(A)…) = REDO(A)
Idempotenz der REDO-Phase
- 对每个 Log-Eintrag E, 如果实际上进行了 REDO, 就会将 E 的 LSN 记录到受影响的页面. 也就是说, 每个页面都记录了最后进行的 REDO 操作.
- 这样是为了防止的 REDO 阶段崩溃后, 新的 REDO 意外触及 AFIM
Idempotenz der UNDO-Phase
- 每执行一次 UNDO, 就会记录一个 CLR(Compensation Log Record), 其中包括一下信息
- LSN
- 涉及的 TA 的 ID
- 更改了的 页面 的 ID
- 该 UNDO 操作的 REDO 信息
- 如果在 UNDO 阶段出现错误, 会在 REDO 阶段执行记录中的 REDO 信息, 并在随后的 UNDO 阶段跳过(因此CLR记录了指向 属于这个TA的, 在补偿操作之前的更改 的LSN 的指针)
# Integrity
# Integrity Constraints
de. Integritätbedingungen 数据库必须始终满足的条件, (通常/建议)由 DBMS 监督维持
约束的种类
- key integrity: 如 key 的唯一性
- referential integrity: 如引用其他表的外键必须存在于该表
- multiplicity constraint: 如维持 1:m 关系中的倍数关系(e.g. 涉及外键更改)
- general constraint: 如属性的值域
Statisches Constraint 定义了可能的 DB 状态, 例如属性的值域
Dynamisches Constraint 定义可能的更新路径(Update-Operation)
# Declarative Constraints
在大多关系型数据库中实现, 如 primary key, unique, foreign key, not null, check. 问题: 在应用这些约束时, 通常需要在程序中定义和实现 => 因此需要
- 是 Schemadefinition 的一部分(create table …)
- e.g. SQL, SQL
- 属性相关/表相关
- 在设计语言中通常是用 Prädikatenlogik 1.Stufe 描述
- (UNIQUE Raum) IB$_1$ : $\forall$ r$_1$ $\in$ Raum(∀r$_2$ $\in$ Raum (r$_1$ [R_ID]= r$_2$ [R_ID] ⇒ r$_1$ = r$_2$ ))
# Überwachung von Integritätsbedingungen durch das DBMS
- $S$ Datenbankschema
- $I$ Integrity constraint
- $IB$ Menge von $I$ über dem Schema $S$
- $DB$ Instanz von S, 现在的 DB状态
- $U$ Update Transaction
- $U(DB)$ 执行完 U 的 DB 状态
- check($I$, $DB$) 检查 DB 状态是否满足 I
# 什么时候检查条件?
方法一: 定期检查所有条件
|
|
问题:
- 撤回很耗时
- 会丢失正确的更新
- 对不 consistent 的数据的读取访问不能取消
方法二: 在 Update 时 增长式检查 前提: 更新是在 consistent 的 DB 状态下进行的
|
|
问题: 测试所有约束很昂贵 => 只测试受影响的 IC
# 检查什么?
示例: referential integrity
- 已知: S 的外键 $\beta$ 用了 R 的主键 $\alpha$
- 那么需要满足的是: (s.$\beta$ 只有 null 值) 或 (对每个 s.$\beta$ 的 非null值 都有 s.$\beta$ = r.$\alpha$)
- 然后课件 dbs1_10c 给了个推导
# Wertenbedingungen(check)
|
|
- 如果 check 表达式被评估为未知, 算 true (与 where 相反)
一个复杂一点的例子: 只有听了课的学生才能考试
 (实际上几乎不支持, 解决方案是)
(实际上几乎不支持, 解决方案是)
# Procedural Constraints(Trigger)
直接在 DDL 中设置简单的 Integrity Constraints(declarative), 通过触发机制支持更复杂的 IC.
# Trigger
- 与表关联且由特定事件触发的行为(通常是PL/SQL程序)
- 包含代码, 测试条件, 然后启动行为
- 可能的触发事件: insert, update, delete
- 可能的时间
- 一个 Integrity Constraint (很)可能有多个 Trigger
# Trigger 种类
- Statement trigger(Befehls-):
- 每个触发命令执行一次
- 通过前缀 new./old. 可以获取 Datensatz 在某个事件前/后的实例
- Row trigger(Datensatz-):
- 对每条更改了(update/insert/delete)的记录执行一次
- 通过 newtable/oldtable 可以获取 触发命令 的更改
# 示例
Tigger Programm 的组建过程

创建 Trigger


# 关于创建唯一的 ID 序列


# Trigger 的一般流程
TA 的 语句 S 中的 Event e 触发了一组 Trigger T = T1, …, tk)
- 将 T1, …, Tk 加入到 Trigger 队列
- 中断 S
- 计算 new. & old. 或 newtable & oldtable
- 执行所有满足条件的 BEFORE-Trigger
- 执行 S 中指定的更新
- 执行所有满足条件的 AFTER-Trigger
P.S. 如果 Trigger 又触发了 Trigger, 嵌套执行这套流程
# safe trigger
- 如果一组触发器总是 terminal, 则被称为安全的(safe, sicher).
- 通常很难测试是否 safe
# Trigger 可以做什么
- 创建完整性条件和创建唯一的 ID
- 执行业务流程(如进行预定时, 应发送一封确认邮件)
- 监测数据库的变化
- 管理临时储存的数据/管理 dauerhaft materialisierter Daten (z.B.
materialisierte Views)
